Принцип действия

4.1.1 Добротность цепи представляет собой безразмер­ную величину, равную произведению 2я на отно­шение запасенной в цепи энергии к энергии, рассеиваемой цепью за время, соответствующее одному периоду колебаний. Это определение можно записать' в виде следующего уравнения:

энергия, запасенная в контуре

Q=2×p ---------------------------------------

энергия, теряемая контуром за один период

Добротность контура, выведенная на основании этого выражения и выраженная через сосредоточенные па­раметры, имеет вид:

, (П.13.3)

где L и С — соответственно индуктивность и емкость контура;

r — эквивалентное сопротивление потерь контура при резонансе;

w— частота.

4.1.2 В измерителе добротности измеряемый индуктив­ный объект образует с конденсатором перемен­ной емкости последовательный колебательный контур, в который ЭДС вводится через трансфор­матор связи (рис. 3). Конструкция этого транс­форматора выполнена так, что вносимое им в колебательный контур сопротивление пренебре­жимо мало. Напряжение на конденсаторе пере­менной емкости С измеряется стрелочным при­бором, шкала которого проградуирована в зна­чениях добротности.

Найдем условия, при которых напряжение на кон­денсаторе контура будет наибольшим.

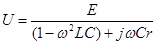(П.13.4)

Переходя к модулю, найдем, что

(П.13.5)

Наибольшее напряжение на контуре будет в том слу­чае, когда знаменатель выражения (П.13.5) станет мини­мальным. Это условие выполняется, когда емкость

(П.13.6)

С учетом выражения (П.13.6) наибольшеенапряжение на конденсаторе при его настройке будет:

(П.13.7)

где — добротность контура.

Извыражения (П.13.7) следует, что

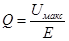(П.13.8)

где Е — ЭДС, вводимая в контур.

Если пренебречь в подкоренном выражении(П.13.7) едини­цей, то добротность контура, определяемая выраже­нием (П.13.8), измеряется с погрешностью менее0,5% при Q > 10.

Физический смысл выражений (П.13.5) и (П.13.7) состоит в том, что если индикатор тока позволяет находить макси­мальный ток в контуре, который совпадает с момен­том наступления собственного резонанса контура при частоте w₀, то индикаторы напряжения позволяют фиксировать момент наибольшего напряжения U_макс на контуре при частоте w_макс, несколько отличной от ре­зонансной частоты w₀.

Частота, которой соответствует наибольшее напряже­ние на контуре, определяется выражением:

(П.13.9)

У контуров с добротностью Q³10 отличие w_максот w₀ не более 1 %. При добротностях Q<10, когда нуж­но знать действительную резонансную частоту, можно найти ее из выражения:

(П.13.10)

Рисунок 3 - Схема последовательного колебательногоконтура

4.1.3 Как отмечалось, сопротивление r (рис. 3) явля­ется общим сопротивлением потерь всего кон­тура. Эти потери включают сопротивление по­терь исследуемого объекта, потерь в конденсато­ре переменной емкости и токоведущих соедини­тельных элементах, потерь в клеммах.

Таким образом, измеряемое значение Q является доб­ротностью всего колебательного контура. Однако, конструкция измерительного конденсатора вы­полнена так, что потери в нем всегда значительно меньше потерь в исследуемом объекте.

Поэтому, показания измерителя добротности можно считать практически свободными от влияния потерь в колебательном контуре измерительного блока в пре­делах погрешностей измерения, оговоренных в разде­ле 3. Это позволило проградуировать шкалу вольтметра измерителя добротности непосредственно в единицах добротности.

Дата добавления: 2015-10-29