Операторный метод решения

Систем дифференциальных уравнений

Зададим параметры ДПТ в MathCAD:

Операторные матрицы:

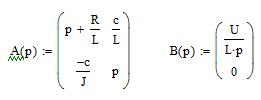
Решение операторной системы уравнений методом обратной матрицы:

Применяя обратное преобразование Лапласа, получаем временные зависимости тока якоря и скорости вращения вала двигателя.

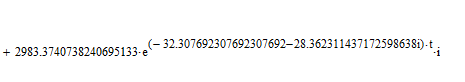
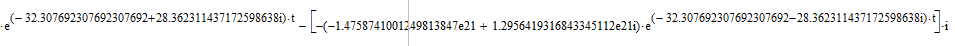
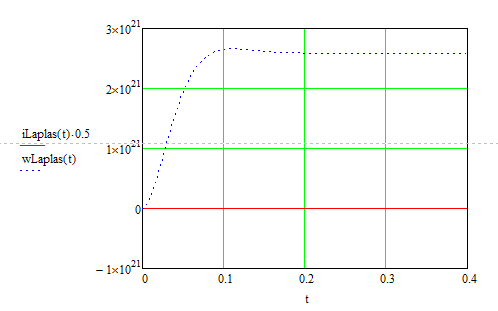
Рисунок 6 - Переходные процессы в ДПТ НВ при решении СДУ

операторным методом

Решение систем дифференциальных уравнений

С применением определителей Вандермонда

Зададим параметры ДПТ в MathCAD:

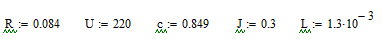
Матрицы коэффициентов и единичная матрица:

Корни характеристического уравнения:

Матрицы Вандермонда:

Матричная функция:

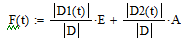
Вектор переменных состояния ДПТ НВ:

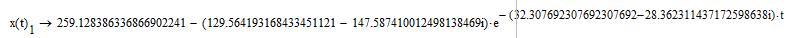
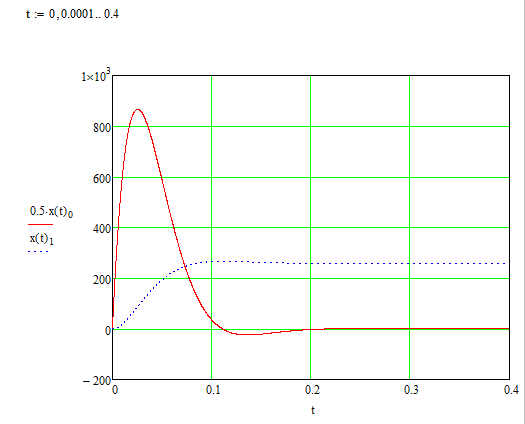
Рисунок 7 - Переходные процессы в ДПТ НВ при решении СДУ

методом определителей Вандермонда

Вывод: В ходе лабораторной работы №2 была исследована динамика ДПТ НВ с помощью различных методов решения дифференциальных уравнений. Были использованы следующие методы: метод Эйлера, классический, операторный, определители Вандермонда.

По результатам решений при применении различных методов были построены динамические характеристик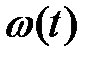и и 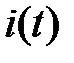. Данные характеристики совпадают во всех четырех случаях. Уравнения решались при нулевых начальных условиях (ДПТ НВ работал на холостом ходу).

Операторный метод является наиболее удобным методом решения по сравнению с классическим, так как для учета начальных условий и нахождения постоянных интегрирования составлялась и решалась отдельная СЛАУ, а при применении преобразования Лапласа можно учитывать начальные условия на самом первом этапе решения СДУ, при этом полученная СЛАУ ненамного отличается от же СЛАУ при нулевых начальных условиях.

Удобным методом для решения СДУ является метод определителей Вандермонда, однако он используется только при нулевых начальных условиях.

Дата добавления: 2015-10-29