
Читайте также:
|
Curves of the second order in plane: theorem on canonic forms (case B ¹ 0). Degenerate curves.
Let an orthonormal system of coordinates 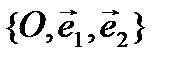 and some curve
and some curve  be given on a plane.
be given on a plane.
A curve  is called an algebraic curve of the second order if its equation in a given system of coordinates has the form:
is called an algebraic curve of the second order if its equation in a given system of coordinates has the form: 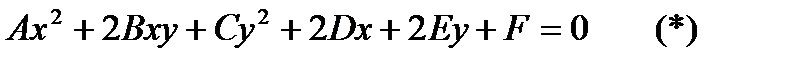
where numbers 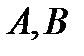 and
and 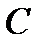 are not equal to zero simultaneously (
are not equal to zero simultaneously (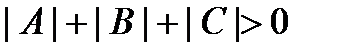 ), and
), and 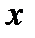 and
and 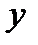 are the coordinates of the radius-vector of a point lying in the curve
are the coordinates of the radius-vector of a point lying in the curve 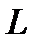 .
.
Introduce the following notation: 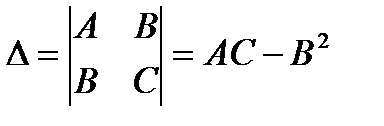 .
.
Theorem 1. For every curve of the second order there exists an orthonormal system of coordinates 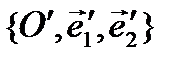 in which an equation of this curve has (for
in which an equation of this curve has (for 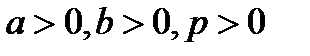 ) one of the following nine (called canonic) forms:
) one of the following nine (called canonic) forms:
| Type of curve | 
| 
| 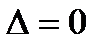
|
| Empty sets | 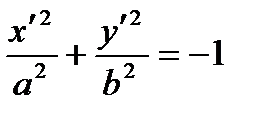
| 
| |
| Points | 
| ||
| Coinciding lines | 
| ||
| Non-coinciding lines | 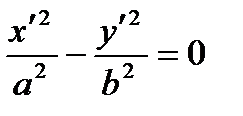
| 
| |
| Curves | Ellipse

| Hyperbola
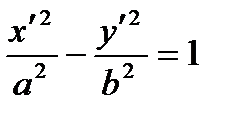
| Parabola
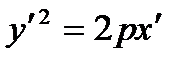
|
Proof: 1. Beforehand we notice that without loss of generality we can assume the following:  and
and  . Indeed, if
. Indeed, if  then we can change the signs of all coefficients in the equation (*). If
then we can change the signs of all coefficients in the equation (*). If  then by transiting to a new orthonormal system of coordinates for which
then by transiting to a new orthonormal system of coordinates for which 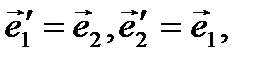
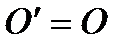 we obtain the desired equation since at this transition the equalities
we obtain the desired equation since at this transition the equalities 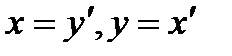 hold. Observe also that
hold. Observe also that 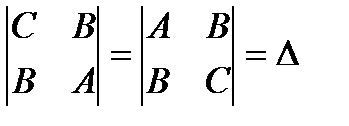 .
.
4. If 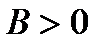 then we transit to a new system of coordinates obtained from the original one by turning around the point
then we transit to a new system of coordinates obtained from the original one by turning around the point  on angle
on angle  such that the coefficient at the product
such that the coefficient at the product  will be equal to zero. Let's deduce a choice rule of this angle. Consider a turning:
will be equal to zero. Let's deduce a choice rule of this angle. Consider a turning:
 with
with  and consequently
and consequently  .
.
Substituting expressions for “old” coordinates by “new”, we obtain the equation (*) in the form:
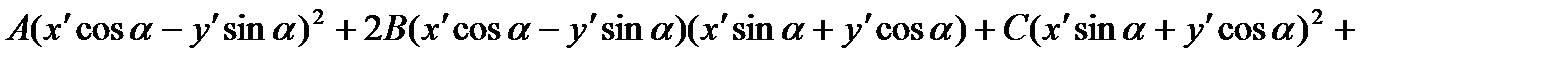
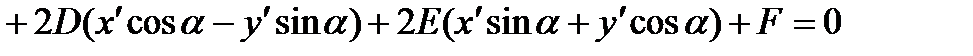
or 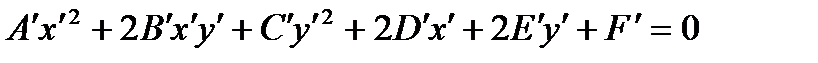 .
.
Then we have 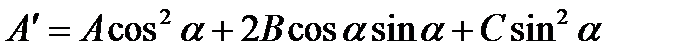
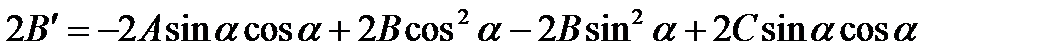
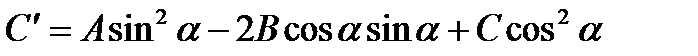
Ellipse, hyperbola, parabola and their properties.
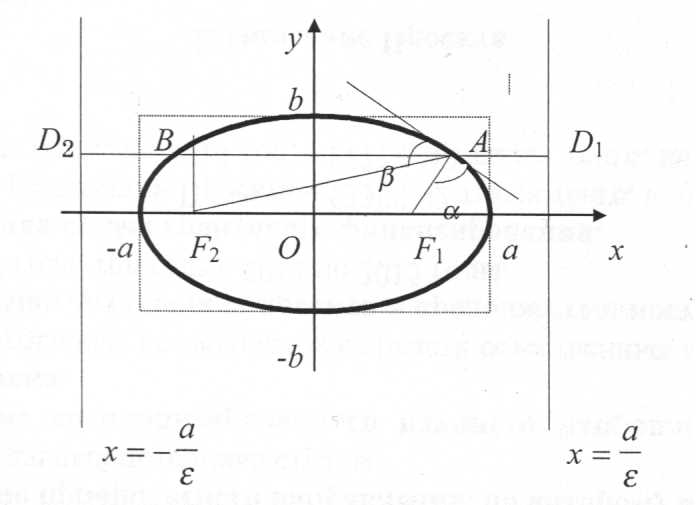 A curve of which the equation in some orthonormal system of coordinates is
A curve of which the equation in some orthonormal system of coordinates is 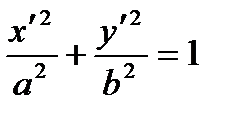 ,
,  , is called an ellipse. The number
, is called an ellipse. The number 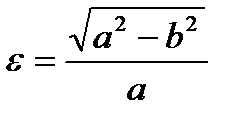 is the eccentricity of an ellipse. The points
is the eccentricity of an ellipse. The points 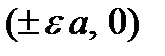 are the focuses of an ellipse. The lines
are the focuses of an ellipse. The lines 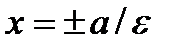 are the directrices of an ellipse. The number
are the directrices of an ellipse. The number  is the focal parameter of an ellipse.
is the focal parameter of an ellipse.
Properties of an ellipse: 1. An ellipse is a restricted curve:  and
and 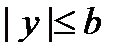 that follows from the record of canonic equation in the form:
that follows from the record of canonic equation in the form:  .
.
2. An ellipse  has axial symmetry regarding to the axes
has axial symmetry regarding to the axes 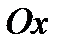 and
and 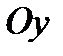 and also central symmetry regarding to the origin of coordinates. This follows from:
and also central symmetry regarding to the origin of coordinates. This follows from: 

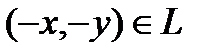 .
.
Denote by 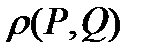 the distance between geometric objects
the distance between geometric objects 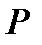 and
and  , and denote by
, and denote by 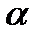 and
and  the angles between the tangent and focal radiuses
the angles between the tangent and focal radiuses  and
and 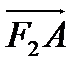 .
.
A curve of which the equation in some orthonormal system of coordinates is 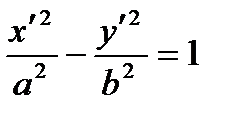 ;
; 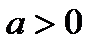 ,
, 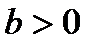 , is called a hyperbola. The number
, is called a hyperbola. The number  is the eccentricity of a hyperbola. The points
is the eccentricity of a hyperbola. The points 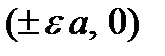 are the focuses of a hyperbola. The lines
are the focuses of a hyperbola. The lines 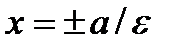 are the directrices of a hyperbola. The number
are the directrices of a hyperbola. The number  is the focal parameter of a hyperbola.
is the focal parameter of a hyperbola.
Properties of a hyperbola: 1. A hyperbola is a unrestricted curve existing for 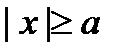 that follows from the record of canonic equation in the form:
that follows from the record of canonic equation in the form:  .
.
2. A hyperbola  has axial symmetry regarding to the axes
has axial symmetry regarding to the axes 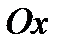 and
and 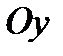 and also central symmetry regarding to the origin of coordinates. This follows from:
and also central symmetry regarding to the origin of coordinates. This follows from: 

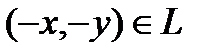 .
.
Denote by  and
and  the angles between the tangent and focal radiuses.
the angles between the tangent and focal radiuses.
A curve of which the equation in some orthonormal system of coordinates is 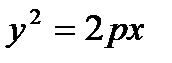 ;
; 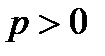 , is called a parabola. The point
, is called a parabola. The point 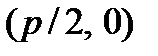 are the focus of a parabola. The line
are the focus of a parabola. The line  are the directrix of a parabola. The number
are the directrix of a parabola. The number  is the focal parameter of a parabola.
is the focal parameter of a parabola.

Denote by 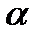 the angle between the tangent and focal radius and by
the angle between the tangent and focal radius and by  – the angle between the tangent and positive direction of the abscissa axis.
– the angle between the tangent and positive direction of the abscissa axis.
Properties of a parabola: 1. A parabola is a unrestricted curve existing for every 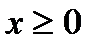 ;
;
2. A parabola  has axial symmetry regarding to the axis
has axial symmetry regarding to the axis 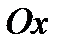 that follows from:
that follows from:
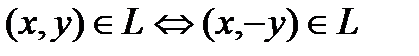 .
.
Дата добавления: 2015-10-29; просмотров: 192 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Интересные клинические случаи | | | Surfaces of the second order in the space: cylindrical and conic surfaces, surfaces of rotation. |