Основные этапы математического моделирования

По целям исследований

В зависимости от целей исследования выделяют следующие модели:

§ функциональные. Предназначены для изучения особенностей работы (функционирования) системы, её назначения во взаимосвязи с внутренними и внешними элементами;

§ функционально-физические. Предназначены для изучения физических (реальных) явлений, используемых для реализации заложенных в систему функций;

§ модели процессов и явлений, такие как кинематические, прочностные, динамические и другие. Предназначены для исследования тех или иных свойств и характеристик системы, обеспечивающих её эффективное функционирование.

3) Основные виды моделей.

Эвристические модели

Эвристические модели, как правило, представляют собой образы, рисуемые в воображении человека.
Эвристическое моделирование — основное средство вырваться за рамки обыденного и устоявшегося. Но способность к такому моделированию зависит, прежде всего, от богатства фантазии человека, его опыта и эрудиции. Эвристические модели используют на начальных этапах проектирования или других видов деятельности, когда сведения о разрабатываемой системе ещё скудны. На последующих этапах проектирования эти модели заменяют на более конкретные и точные.

Натурные модели

Отличительной чертой этих моделей является их подобие реальным системам (они материальны), а отличие состоит в размерах, числе и материале элементов и т. п. По принадлежности к предметной области модели подразделяют на следующие:

§ Физические модели. Это — реальные изделия, образцы, экспериментальные и натурные модели, когда между параметрами системы и модели одинаковой физической природы существует однозначное соответствие. Выбор размеров таких моделей ведется с соблюдением теории подобия.

Математические модели

Математические модели — формализуемые, то есть представляют собой совокупность взаимосвязанных математических и формально-логических выражений, как правило, отображающих реальные процессы и явления (физические, психические, социальные и т. д.). По форме представления бывают:

§ аналитические модели. Их решения ищутся в замкнутом виде, в виде функциональных зависимостей. Удобны при анализе сущности описываемого явления или процесса и использовании в других математических моделях, но отыскание их решений бывает весьма затруднено;

§ численные модели. Их решения — дискретный ряд чисел (таблицы). Модели универсальны, удобны для решения сложных задач, но не наглядны и трудоемки при анализе и установлении взаимосвязей между параметрами. В настоящее время такие модели реализуют в виде программных комплексов — пакетов программ для расчета на компьютере. Программные комплексы бывают прикладные, привязанные к предметной области и конкретному объекту, явлению, процессу, и общие, реализующие универсальные математические соотношения (например, расчет системы алгебраических уравнений);

§ формально-логические информационные модели — это модели, созданные на формальном языке.

4) Основные свойства моделей

- целенаправленность - модель всегда отображает некоторую систему, т.е. имеет цель;

- конечность - модель отображает оригинал лишь в конечном числе его отношений и, кроме того, ресурсы моделирования конечны;

- упрощенность - модель отображает только существенные стороны объекта и, кроме того, должна быть проста для исследования или воспроизведения;

- упрощенность - модель отображает только существенные стороны объекта и, кроме того, должна быть проста для исследования или воспроизведения;

- адекватность - модель должна успешно описывать моделируемую систему;

- наглядность, обозримость основных ее свойств и отношений;

- доступность и технологичность для исследования или воспроизведения;

- информативность - модель должна содержать достаточную информацию о системе (в рамках гипотез, принятых при построении модели) и должна давать возможность получить новую информацию;
- полнота - в модели должны быть учтены все основные связи и отношения, необходимые для обеспечения цели моделирования

- управляемость (имитационность) - модель должна иметь хотя бы один параметр, изменениями которого можно имитировать поведение моделируемой системы в различных условиях;

5) Основные принципы моделирования

Модель должна строится так, чтобы она наиболее полно воспроизводила те качества объекта, которые необходимо изучить в соответствии с поставленной целью. Во всех отношениях модель должна быть проще объекта и удобнее его для изучения. таким образом, для одного и того же объекта могут существовать различные модели, классы моделей, соответствующие различным целям его изучения.

Необходимым условием моделирования является подобие объекта и его модели.

Основные этапы математического моделирования

1) Построение модели. На этом этапе задается некоторый «нематематический» объект — явление природы, конструкция, экономический план, производственный процесс и т. д. При этом, как правило, четкое описание ситуации затруднено. Сначала выявляются основные особенности явления и связи между ними на качественном уровне. Затем найденные качественные зависимости формулируются на языке математики, то есть строится математическая модель. Это самая трудная стадия моделирования.

2) Решение математической задачи, к которой приводит модель. На этом этапе большое внимание уделяется разработке алгоритмов и численных методов решения задачи на ЭВМ, при помощи которых результат может быть найден с необходимой точностью и за допустимое время.

3) Интерпретация полученных следствий из математической модели. Следствия, выведенные из модели на языке математики, интерпретируются на языке, принятом в данной области.

4) Проверка адекватности модели. На этом этапе выясняется, согласуются ли результаты эксперимента с теоретическими следствиями из модели в пределах определенной точности.

5) Модификация модели. На этом этапе происходит либо усложнение модели, чтобы она была более адекватной действительности, либо ее упрощение ради достижения практически приемлемого решения.

8) Источник возникновения погрешностей можно проследить, следуя вышеприведенным этапам численного решения задачи. Во-первых, это погрешность, вносимая математической моделью задачи. Величина погрешности, вносимой в результат математической моделью, может возрасти, если в модели не учтены какие-либо важные характеристики изучаемого явления.

Кроме того, исходные данные вносят свою долю (иногда основную) в образование погрешности результата.

Эти источники погрешности называют неустранимыми погрешностями, так как их нельзя полностью устранить ни до начала решения задачи, ни, тем более, в процессе ее решения.

Не следует стремиться к уменьшению погрешности одних данных, оставляя другие без изменени

Еще одним источником погрешности является численный метод. Во многих численных методах, связанных,например, с приближенным вычислением интегралов или с нахождением промежуточных значений функции, заданной в виде таблицы, используется идея приближения функции с помощью алгебраического многочлена

9) Понятие сигналов. Основные функции сигналов.

сигналом называется материальный носитель информации, используемый для передачи сообщений по системе связи. Сигналом может быть любой физический процесс, параметры которого изменяются в соответствии с передаваемым сообщением.

Понятие сигнал позволяет абстрагироваться от конкретной физической величины, например тока, напряжения, акустической волны и рассматривать вне физического контекста явления связанные кодированием информации и извлечением ее из сигналов, которые обычно искажены шумами. В исследованиях сигнал часто представляется функцией времени, параметры которой могут нести нужную информацию. Способ записи этой функции, а также способ записи мешающих шумов называют математической моделью сигнала.

Любое автоматическое устройство представляет собой комплекс отдельных конструктивных или схемных элементов, каждый из которых выполняет задачу по преобразованию энергии, полученной от предыдущего элемента, и передаче ее последующему элементу. Элементами автоматики называются конструктивно законченные устройства, выполняющие определенные самостоятельные функции преобразования сигнала (информации) в системах автоматического управления и контроля.

11) Динамический объект (от дина - сила, т.е. объект, воспринимающий силу, воздействие) это физическое тело, техническое устройство или процесс, имеющее входы, точки возможного приложения внешних воздействий, и воспринимающие эти воздействия, и выходы, точки, значения физических величин в которых характеризуют состояние объекта. Объект способен реагировать на внешние воздействия изменением своего внутреннего состояния и выходных величин, характеризующих его состояние. И воздействие на объект, и его реакция в общем случае изменяются с течением времени, они наблюдаемы, т.е. могут быть измерены соответствующими приборами. Объект имеет внутреннюю структуру, состоящую из взаимодействующих динамических элементов. Понятие динамический объект содержит и выражает причинно-следственную связь между воздействием на него и его реакцией. Например, между силой, приложенной к массивному телу, и его положением и движением, между электрическим напряжением, приложенным к элементу, и током, протекающем в нем.

12) Идентификация систем.

Идентификация систем — математический аппарат для построения математических моделей динамической системы по измеренным данным. Математическая модель в данном контексте означает математическое описание динамики поведения какой-либо системы или процесса в частотной или временной области, к примеру, физических процессов (движение механической системы под действием силы тяжести), экономического процесса (реакция биржевых котировок на внешние возмущения) и т.п. В настоящее время эта область теории управления хорошо изучена и находит широкое применение на практике.

13) Активная и пассивная идентификация.

Методы идентификации принято разделять на две группы:

· активная идентификация – идентификация вне контура управления,

· пассивная идентификация – идентификация в контуре управления.

Активная идентификация

· В этом случае объект исследования выводится из условий нормальной окружающей среды (нормальный режим эксплуатации, номинальные параметры рабочего режима и т. п.). Исследования проводятся в специализированных лабораторных условиях

· Активную идентификацию используют при разработке новых технологий применительно к действующим промышленным объектам, в изучении новых явлений, в первоначальной разработке математической модели.

Пассивная идентификация

· При пассивной идентификации объект функционирует в контуре управления, находится в процессе нормальной эксплуатации. На его входы поступают только естественные сигналы управления.

· Пассивную идентификацию используют для уточнения математической модели, для слежения за изменениями в объекте. Информация оперативно используется в системе управления объектом.

14) Параметрическая и структурная идентификация.

Структурная идентификация представляет собой определение

вида уравнений, описывающих процессы в ЭМУ, а параметрическая — выявле-

ние характера некоторых функциональных зависимостей и определение значе-

ний конкретных параметров.

15) Виды моделей объектов управления.

Объект управления- обозначающий устройство или динамический процесс, управление поведением которого является целью создания системы автоматического управления.

Классификация моделей объектов управления

Существует большое разнообразие типов и классов моделей.

. СМ ВОПРОС 3

16) Импульсная характеристика.

Импульсная характеристика показывает реакцию дискретной системы на подачу на ее вход единичной импульсной функции.

Импульсная характеристика является основной характеристикой линейной системы: зная ее можно определить реакцию на любое воздействие.

17) Переходная функция.

Переходная характеристика h(t) - это реакция системы на входное единичное ступенчатое воздействие при нулевых начальных условиях.

одна из осн. хар-к линейной системы, к-рая полностью определяет её динамич. св-ва. Зная П. ф. системы, можно заранее определить, как эта система будет реагировать на любое воздействие.

18) Если на вход объекта подавать периодический сигнал заданной амплитуды и частоты, то на выходе будет также периодический сигнал той же частоты, но в общем случае другой амплитуды со сдвигом по фазе. Взаимосвязь между параметрами периодических сигналов на входе и выходе объекта определяют частотные характеристики. Чаще всего их используют для описанияодноканальных систем

19) Модель для переменных состояния.

Пространство состояний — в теории управления один из основных методов описания поведения динамической системы

В пространстве состояний создаётся модель динамической системы, включающая набор переменных входа, выхода и состояния, связанных между собой дифференциальными уравнениями первого порядка, которые записываются вматричной форме. В отличие от описания в виде передаточной функции и других методов частотной области, пространство состояний позволяет работать не только с линейными системами и нулевыми начальными условиями.

20) По законам математики, любую (почти) функцию можно разложить в ряд Фурье, то есть, на сумму синусоид с различной фазой и амплитудой. Эти синусоиды называются "гармониками". Каждая гармоника имеет как бы свой вес в исходном сигнале. Совокупность этих весов называется "спектром". Нахождение спектра -- и есть спектральный анализ.

Иногда на спектре становится очень заметным что-то такое, чего по исходному сигналу сказать нельзя.

Если провести спектральный анализ, например, звука человеческого голоса, то в нём обнаружится основной тон (это высота голоса) и обертоны, определяющие его тембр.

1. 21) Прямое преобразование Фурье.

Прямое преобразование Фурье имеет вид:

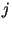здесь -- некоторая функция, -- мнимая единица. Это преобразование часто записывают в форме:

(П34)

Исходная независимая переменная измеряется, как правило, в секундах, а получаемая независимая переменная -- в герцах. Преобразование Фурье существует, если выполняется условие абсолютной интегрируемости функции :

22) Обратное преобразование Фурье.

Обратное преобразование Фурье записывается в виде:

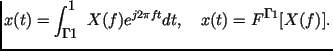
(П36)

С преобразованием Фурье тесно связано понятие дельта-функции (функции Дирака). Это функция, график которой имеет бесконечную высоту, нулевую ширину и площадь, равную единице. Математическое определение дельта-функции имеет вид:

(П37)

С помощью математической операции (1.37) из непрерывного процесса выделяется одна точка , соответствующая моменту времени .

23) Внешние воздействия, как отмечалось в п. 1.1 могут быть полезными

(управляющими сигналами u) и помехами (возмущающими воздействиями f).

Управляющие сигналы, вырабатываемые устройством управления, являются

полностью наблюдаемыми. Возмущающие воздействия, в отличие от них, как

правило, ненаблюдаемые и случайные сигналы

Для количественной оценки и сравнения различных случайных сигналов

используют различные характеристики этих сигналов, представляющие собой

абстрактные математические понятия, которые существуют объективно, но не

могут быть измерены или определены в строгом смысле слова.

К таким характеристикам относятся1. Функция распределения вероятностей случайного процесса, или

интегральная функция распределения.

2. Плотность вероятностей, или дифференциальное распределение

(распределение)

3. Математическое ожидание случайного процесса

24)

Помехи, приводят к тому,что искаженный сигнал отличается от полезного сигнала, полученного отисточника сообщения y(t), и в общем случае имеет вид

y(t) = x(t) + e(t). Где e(t) – аддитивнаясоставляющая. (сигнал рассовачования)

адитивное - это вообще всё то, что ПРИБАВЛЯЕТСЯ к чему-то нужному или основному. Поэтому аддитивная помеха - та, которая просто суммируется с полезным сигналом.

25) Типы помех.

помехи — сигналы, не связанные с источниками информации о задачах и результатах управления.

Основные виды:

Аддитивные - это вообще всё то, что ПРИБАВЛЯЕТСЯ к чему-то нужному или основному. Поэтому аддитивная помеха - та, которая просто суммируется с полезным сигналом.
Может быть ещё, например, и

мультипликативная помеха - та, на которую умножается полезный сигнал (появляется паразитная амплитудная модуляция).

26) Постановка задачи оптимального управления.

Оптимальное управление — это задача проектирования системы, обеспечивающей для заданного объекта управления или процесса закон управления или управляющую последовательность воздействий, обеспечивающих максимум или минимум заданной совокупности критериев качества системы

Для решения задачи оптимального управления строится математическая модель управляемого объекта или процесса, описывающая его поведение с течением времени под влиянием управляющих воздействий и собственного текущего состояния

27) Программное оптимальное управление

Программное оптимальное управление – это решение задачи оптимального управления математической теории, в к-рой управляющее воздействие u=u (t).формируется в виде функции времени (тем самым предполагается, что по ходу процесса никакой информации, кроме заданной в самом начале, в систему не поступает). Таким образом, О. у. п. формируется по априорным сведениям о системе и уже не может быть скорректировано.

28-29) Невозмущённое и возмущённое движение динамической системы

Невозмущенное движение – это заданное движение системы при определенных начальных условиях. Вследствие различных возмущающих воздействий, действующих на систему, фактическое движение будет отличаться от заданного невозмущенного движения.

Так как реальное движение системы неизбежно отличается от номинального

программного, то этот факт привел к концепции невозмущенного и возмущенного

движений Ляпунова. Так, любое программное движение системы,

независимо от того является ли оно оптимальным или допустимым называется

невозмущенным движением. Возмущенное движение оценивается при этом

некоторыми отклонениями от невозмущенного движения. Следовательно,

возмущенное движение будет описываться следующими переменными

30) Принцип динамического программирования Беллмана

Уравнение Беллмана (также известное как уравнение динамического программирования)- Он заключается в том, что на каждом шаге следует стремиться не к изолированной оптимизации функции f_k(х_k, ξ_k), а выбирать оптимальное управление х_k* в предположении об оптимальности всех последующих шагов.

31) Принцип динамического программирования отнюдь не предполагает, что каждый шаг оптимизируется отдельно, независимо от других. Напротив, шаговое управление должно выбираться дальновидно, с учетом всех его последствий в будущем. Что толку, если мы выберем на данном шаге управление, при котором эффективность этого шага максимальна, если этот шаг лишит нас возможности хорошо выиграть па последующих шагах. оптимальное управление обладает тем свойством, что для любого начального состояния и использованного начального управления последующее оптимальное управление совпадает с исходным оптимальным управлением относительно состояния, получающегося в результате применения начального управления. (ответ 30 вопрос)

Дата добавления: 2015-10-29