
|
Читайте также: |
ЛАБОРАТОРНАЯ РАБОТА №1
отчет
по дисциплине «Численные методы»
Одномерные и двумерные сплайны
Студент
__________ Рыбин А.В.
(Подпись) (Фамилия, И., О.)
_ 10-ПМ _________
(Группа) (Дата сдачи)
Студент
__________ Хитева Д.В.
(Подпись) (Фамилия, И., О.)
_ 10-ПМ _________
(Группа) (Дата сдачи)
Проверила
__________ Катаева Л.Ю.
(Подпись) (Фамилия, И.,О.)
Отчет защищён «____»_________2013г.
с оценкой____________________
Н. Новгород, 2013
Оглавление
Постановка задачи. 3
Теоретический материал. 4
Таблица идентификаторов. 6
Реализация методов на С++.. 6
Excel 21
Результат работы программ.. 23
Сводная таблица результатов. 27
Вывод. 28
Постановка задачи
Одним из наиболее широко используемых представлений кривых в компьютерном видении является В-сплайн представление. Важно различать сплайны и В-сплайны. В-сплайны являются полиномиальными функциями. Сплайны являются линейной комбинацией В-сплайнов. В литературе сплайны обычно определяются как различные виды степенной функции. Для вычислений более удобно определять сплайны рекурсивными функциями.
Некоторая функция f (x) задана на отрезке  , разбитом на части
, разбитом на части  ,
, 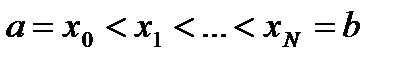 . Кубическим сплайном дефекта 1 называется функция
. Кубическим сплайном дефекта 1 называется функция 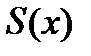 , которая:
, которая:
 является многочленом степени не выше третьей;
является многочленом степени не выше третьей; ;
; выполняется равенство
выполняется равенство 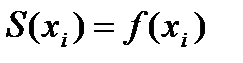 , т. е. сплайн
, т. е. сплайн  интерполирует функцию f в точках
интерполирует функцию f в точках  .
.Для однозначного задания сплайна перечисленных условий недостаточно, для построения сплайна необходимо наложить какие-то дополнительные требования.
Естественным кубическим сплайном называется кубический сплайн, удовлетворяющий также граничным условиям вида:

Таким образом перед нами ставиться задача реализовать построение одномерного кубического сплайна. Так же мы ставим себе задаче реализовать построение двумерного кубического сплайна.
Теоретический материал
Обозначим: 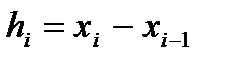 (1)
(1)
На каждом отрезке  функция
функция  есть полином третьей степени
есть полином третьей степени 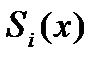 , коэффициенты которого надо определить. Запишем для удобства
, коэффициенты которого надо определить. Запишем для удобства 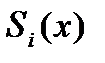 в виде:
в виде:

тогда

Условия непрерывности всех производных до второго порядка включительно записываются в виде

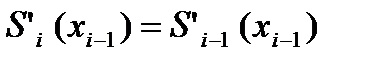

а условия интерполяции в виде

Отсюда получаем формулы для вычисления коэффициентов сплайна:
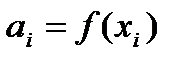
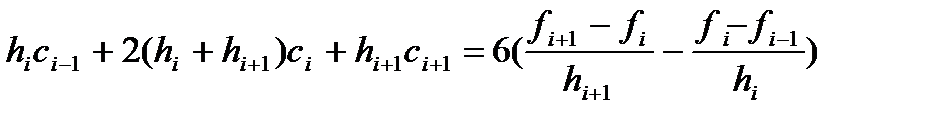
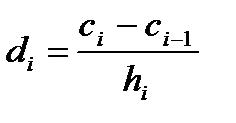

Формулы используемые при реализации одномерного и двумерного сплайна:
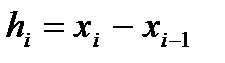 . (1)
. (1)
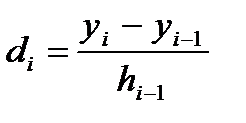 . (2)
. (2)
 . (3)
. (3)
при начальных условиях: 

 (4)
(4)
где N=n-1; n - количество точек.
Из заданных граничных условий, находим:
 (5)
(5)
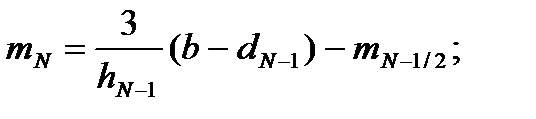 (6)
(6)
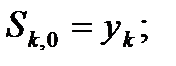
 (7)
(7)
Полученные коэффициенты, это и есть нужные нам коэффициенты полиномов третьей степени.
Таблица идентификаторов
Таблица №1-Одномерный кубический сплайн
| Тип переменной | Имя переменной | Хранимое значение |
| int | n | Кол-во точек |
| int | N | n-1 |
| double | p[][] | Точки, координаты x и y |
| double | a,b | Начальные условия |
| double | m[] | коэффициенты |
| double | S[][] | Коэф-ты полученных уравнений для построения |
Таблица №1-Двумерный кубический сплайн
| Тип переменной | Имя переменной | Хранимое значение |
| int | kk | Кол-во столбцов |
| int | nn | Кол-во строк |
| double | p[][] | Точки, координаты |
| double | sy0,syn,sx0,sxn | Граничные условия |
| double | y0,yn,x0,xn | Начальные и конечные x и y |
| double | z[][] | Исходная матрица высот |
| double | zxy[][] | Итоговая расширенная матрица |
Реализация методов на С++
Одномерный кубический сплайн
| #include <iostream> #include <fstream> using namespace std; int main() { double a,b; // init conditions int n = 0; // кол-во точек int N; //кол-во пар int k = 0; ifstream file; file.open("in.txt"); while (file) { char ch = file.get(); if (ch == '\n') n++; } file.close (); double** p= new double*[n]; for(int i=0;i<n;++i) { p[i]=new double[2]; } file.open("in.txt"); for (int i=0; i < n; ++i) { file>>p[i][0]; file>>p[i][1]; } file.close (); k=n; cout<<n<<endl; cout<<"Enter initial conditions, S'("<<p[0][0]<<") and S'("<<p[n-1][0]<<")"<<endl; cin>>a>>b; cout<<"S'("<<p[0][0]<<")="<< a <<" and S'("<<p[n-1][0]<<")="<< b <<endl<<endl; cout<<"points:"<<endl; for(int i=0;i<n;i++) { cout<<"("<<p[i][0]<<","<<p[i][1]<<")"<<endl; } ///////////////////// double* h = new double [n]; double* d = new double [n]; double* u = new double [n]; double* m = new double [n]; ///////////////////// for(int i=1;i<n;i++) { h[i-1]=p[i][0]-p[i-1][0]; // формула (1) d[i-1]=(p[i][1]-p[i-1][1])/h[i-1]; // формула (2) } for(int i=1;i<n-1;i++) { u[i]=6*(d[i]-d[i-1]); // формула (3) // cout<<u[i]<<endl; } N=n-1; //кол-во пар double** M= new double*[n]; for(int i=1;i<N;++i) { M[i]=new double[n]; } double** S= new double*[n]; for(int i=0;i<k;++i) { S[i]=new double[n]; } // Формулы (4) if(n==4) { for(int i=1;i<N;i++) { if(i==1) { M[1][1]=(3.0/2) * h[0] + 2 * h[1]; M[1][2]=h[1]; M[1][3]=u[1] - 3*(d[0]-a); } if(i>=2 && (N-2)==1) { M[i][1]=h[N-2]; M[i][2]=(2*h[N-2]+(3.0/2)*h[N-2]); M[i][3]=u[N-1]-3*(b-d[N-1]); } } } if(n>4) { for(int i=1;i<N;i++) { if(i==1) { M[1][1]=(3.0/2) * h[0] + 2 * h[1]; M[1][2]=h[1]; for(int j=3;j<n;j++) { M[1][j]=0; } M[1][N]=u[1] - 3*(d[0]-a); } if((i>=2 && i<=N-1) && (N-2)!=1) { for(int j=1;j<n;j++) { if((i-1)!=j && i!=j && (i+1)!=j) { M[i][j]=0; } } M[i][i-1]=h[i-1]; M[i][i]=2*(h[i-1]+h[i]); M[i][i+1]=h[i]; M[i][N]=u[i]; } if(i==N-1) { for(int j=1;j<n;j++) { if((N-2)!=j && (N-1)!=j) { M[i][j]=0; } } M[i][N-2]=h[N-2]; M[i][N-1]=(2*h[N-2]+(3.0/2)*h[N-2]); M[i][N]=u[N-1]-3*(b-d[N-1]); } } } for(int i=1;i<N;i++) { for(int j=1;j<n;j++) { cout<<M[i][j]<<" "; } cout<<endl; } n=n-2; double temp; //прямой ход for(int i=1;i<=n;i++) { for(int j=i+1;j<=n;j++) { temp = (M[j][i])/(M[i][i]); for(int k=1; k<=n+1;k++) { M[j][k]=M[j][k]-M[i][k]*temp; } } } //обратный ход m[n] = M[n][n+1]/M[n][n]; //cout<<n<<endl; for(int i=n-1;i>0;i--) { temp=0; for(int j=i+1;j<=n;j++) { temp = temp + M[i][j]*m[j]; } temp = M[i][n+1] - temp; m[i] = temp/M[i][i]; } // Формулы (5) и (6) m[0]=(3.0/h[0]) * (d[0] - a) - m[1]/2; m[N]=(3.0/h[N-1]) * (b - d[N-1]) - m[N-1]/2; //ответ, вывод значения корней for(int i=0;i<k;i++) { cout<<"m["<<i<<"]="<<m[i]<<endl; } // Формулы (7) for(int i=1;i<k;i++) { S[i-1][0]=p[i-1][1]; S[i-1][1]=d[i-1]-((h[i-1] * (2*m[i-1]+m[i]))/6); S[i-1][2]=m[i-1]/2; S[i-1][3]=(m[i]-m[i-1])/(6*h[i-1]); cout<<"S["<<i-1<<"](x)= ("<< S[i-1][3] <<")*(x - (" <<p[i-1][0]<<"))^3 " <<" + ("<< S[i-1][2] <<")*(x - (" <<p[i-1][0]<<"))^2 + ("<< S[i-1][1] <<")*(x - ("<<p[i-1][0] <<")) + (" << S[i-1][0]<<")"<<endl; } fstream outfile; outfile.open("spline.txt", ios::out); //ios::app ios::in outfile<<k<<" \n"; for(int i=0;i<k;i++) { outfile<<(p[i][0])<<" "; } outfile<<"\n"; for(int i=1;i<k;i++) { outfile<<S[i-1][3]<<" "<<S[i-1][2]<<" "<<S[i-1][1]<<" "<<S[i-1][0]<<" \n"; } outfile.close(); system("pause"); return 0; } |
Дата добавления: 2015-10-29; просмотров: 295 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Evaluate the complete transaction to understand its history and the commercial terms, especially pricing. | | | Повелительные предложения в косвенной речи |