Створення вихідних даних

МЕТОДИЧНІ ВКАЗІВКИ

ДО РОЗРАХУНКОВОЇ РОБОТИ З КУРСУ

“МАТЕМАТИЧНА СТАТИСТИКА”

КИЇВ 2013

Вступ

Розрахункова робота з курсу “Математична статистика” виконуються студентами ІІ курсу спеціальності “Гнучкі комп'ютеризовані системи та робототехніка” стаціонарного та заочного навчання.

Основна мета роботи – закріпити знання, одержані на лекційних, практичних заняттях та в результаті самостійної роботи. Студенти опановують методи та засоби аналізу статистичних даних, розвивають навички використання ЕОМ для розв’язку прикладних задач, освоюють прийоми роботи у математичному програмному пакеті Mathcad 2000.

Зміст розрахункової роботи

Частина 1. Аналіз емпіричної вибірки неперервної випадкової величини

1. Створення вихідних даних

2. Характеристики емпіричної вибірки

2.1. Числові характеристики

2.2. Варіаційний ряд

2.3. Гістограма частот

2.4. Емпірична функція розподілу

3. Статистична оцінка параметрів розподілу

3.1. Точкові оцінки параметрів розподілу

3.1.1. метод моментів

3.1.2. метод найбільшої подібності

3.2. Інтервальні оцінки параметрів розподілу

4. Перевірка статистичних гіпотез

4.1. Перевірка гіпотези про вигляд закону розподілу

4.1.1. перевірка за критерієм Пірсона

4.1.2. перевірка за критерієм Колмогорова

4.1.3. перевірка за критерієм Мізеса (w²)

4.2. Перевірка гіпотез про параметри розподілу

4.2.1. гіпотеза про математичне очікуване

4.2.2. гіпотеза про середнє квадратичне відхилення

У 3 та 4 розділах дослідити залежність оцінок та критеріїв від об’єму вибірки та рівня Рдов. Зробити висновки про виконання закону великих чисел.

Частина 2. Задача регресії

1. Створення вихідних даних

2. Точкові оцінки параметрів рівняння прямої лінії середньоквадратичної регресії

3. Інтервальні оцінки параметрів рівняння прямої лінії середньоквадратичної регресії

Дослідити залежність оцінок параметрів рівняння регресії від об’єму вибірки та стратегії експерименту.

Частина 3. Дисперсійний аналіз

1. Створення вихідних даних

2. Однофакторний дисперсійний аналіз

Варіанти завдань

№	Частина 1	Частини 2 та 3
МХ	σx	y0	β	μ	η
				0,1
				0,2
				0,3
				0,4
				0,5
				0,6
				0,7
				0,8
				0,9
				1,0
				1,1
				1,2
				1,3
				1,4
				1,5
				1,6
				1,7
				1,8
				1,9
				2,0
				-0,4
				-0,5
				-0,6
				-0,7
				-0,8
				-0,9
				-1,0
				-1,1

Методичні вказівки щодо виконання роботи

Частина 1. Аналіз емпіричної вибірки неперервної випадкової величини

Створення вихідних даних

До початку роботи змініть значення системної змінної ORIGIN з 0 на 1 (ця змінна відповідає початковому індексу елементів масивів). Це можна зробити двома способами: через меню Математика/Опції або на початку документу зробити запис

Cпочатку задайте об’єм вибірки та визначте змінну, яка буде використовуватись як індекс(порядковий номер). Наприклад:

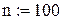
Двокрапку набирайте натисканням кнопки m..n на панелі інструментів “Матриці” або “Арифметика”.

Для створення вихідних даних скористайтеся однією із стандартних функцій генерування даних за певним розподілом імовірності. Для вставки функції скористайтеся кнопкою f (x) панелі інструментів або меню Вставка/Функція. У вікні зліва виберіть групу функцій “Випадкові числа”, а справа – потрібну функцію. Наприклад, для створення вибірки нормальної випадкової величини виберіть функцію rnorm:

Перший параметр функції – об’єм вибірки, другий – математичне очікуване, третій – середнє квадратичне відхилення.

Щоб продивитися створену вибірку, запишіть

Знак транспонування матриці набирайте з панелі інструментів “Матриці”, а не як степінь.

Дата добавления: 2015-10-28