К стоку сети в Excel

Подготовка бланка решения:

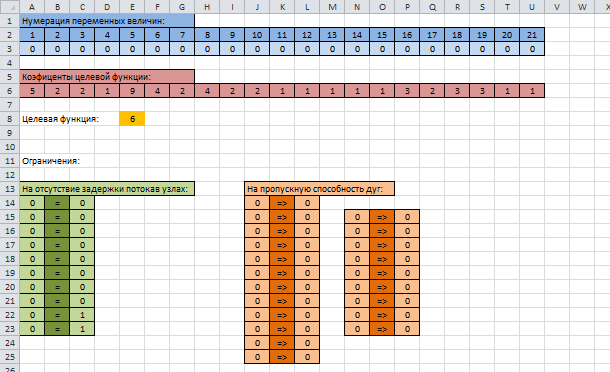
Подготовка бланка решения (в режиме формул):

Заполнение параметров поиска решений:

Устанавливаем параметры:

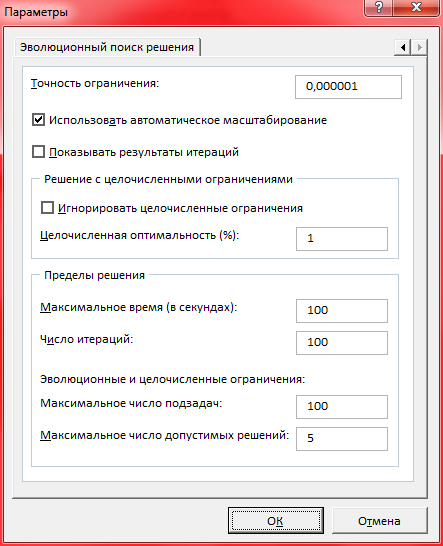
Нажимаем OK → Выполнить → Сохранить найденное решение → OK

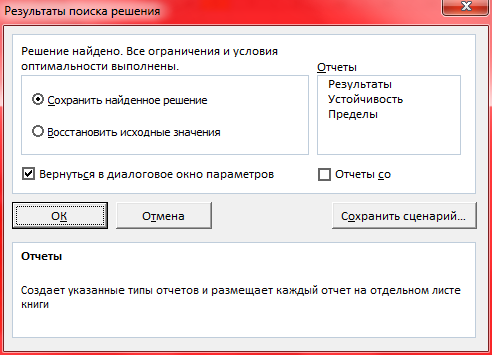
Результат:

5. Решение задачи о «Назначениях рабочих».

Решение задачи о

«Назначениях рабочих» в MathCad.

Так как условия задачи неоднозначны, имеется возможность в двух вариантах интерпретировать ответ. Воспользуемся матрицей из условий:

	Столб. 1	Столб. 2	Столб. 3	Столб. 4	Столб. 5	Столб. 6
Строк.1	3 x1	6 x2	4 x3	5 x4	4 x5	2 x6
Строк.2	1 x7	3 x8	2 x9	1 x10	3 x11	5 x12
Строк.3	5 x13	5 x14	5 x15	5 x16	1 x17	4 x18
Строк.4	4 x19	5 x20	6 x21	7 x22	1 x23	9 x24
Строк.5	2 x25	6 x26	6 x27	6 x28	1 x29	7 x30
Строк.6	5 x31	6 x32	4 x33	5 x34	1 x35	5 x36

Сумма всех элементов строки матрицы, должна быть равной 1, так как сотрудников 6 и их всех примут на работу. Сумма всех элементов одного столбца матрицы тоже, должна быть равной 1, так как на одно рабочее место должен быть назначен один сотрудник.

Общее количество всех назначений можно вычислить как:

Учитываем ограничения:

Получаем задачу оптимизации:

Для большей наглядности преобразуем транспонированный вектор в матрицу:

Матрица показывает, как будут распределены рабочие, например, вариант 1 показывает, что Раб. 1 будет работать на Мест. 5 и т.д. При этом минимальные затраты на производство будут равны 15. Матрица не однозначна, так как дать имена строкам и столбцам можно по-разному:

Вариант 1:

	Раб. 1	Раб. 2	Раб. 3	Раб. 4	Раб. 5	Раб. 6
Мест. 1						+
Мест. 2				+
Мест. 3					+
Мест. 4		+
Мест. 5	+
Мест. 6			+

Вариант 2:

	Мест. 1	Мест. 2	Мест. 3	Мест. 4	Мест. 5	Мест. 6
Раб. 1					+
Раб. 2				+
Раб. 3						+
Раб. 4		+
Раб. 5			+
Раб. 6	+

Из обеих интерпретаций решений видно, что при разном распределении сотрудников на места, затраты на производство по-прежнему будут равны 15.

Решение задачи о

«Назначениях рабочих» в Excel

Подготовка бланка решения:

Подготовка бланка решения (в режиме формул):

Заполнение параметров поиска решений:

Устанавливаем параметры:

Нажимаем OK → Выполнить → Сохранить найденное решение → OK

Результат:

Вывод

Как видно из данной работы, необязательно решать задачи оптимизации вручную. С этой задачей успешно справляются компьютерные программы. Результаты вычислений и в MathCad, и в Excel совпали и оказались достаточно точными.

Задачи, приведённые в этой работе, являются лишь примером. С помощью оптимизации можно решать намного более сложные задачи, MathCad и Excel способны решать их также быстро и точно.

Список используемой литературы.

1. Аносова С.В. Методические указания по использованию MathCad для решения некоторых учебных задач.

2. Ю.Ю. Тарасевич Численные методы на Mathcad’е. – Астраханский гос. Пед. Ун-т: Астрахань, 2000.

3. Поршнев С.В., Беленкова И.В. Численные методы на базе Mathcad. – СПб.: БХВ-Петербург, 2005.

Дата добавления: 2015-10-28