В сети в MathCad.

Оглавление

1. Условия и тексты заданий....……………………………………..………… 3

2. Краткая теория...…………………………………………………………… 4

3. Расчет максимального потока в сети

3.1 Расчет максимального

потока в сети в MathCad …………………………………………………… 5

3.2. Расчет максимального

потока в сети в Excel …..…………………………………………………… 7

4. Поиск минимального пути от источника к стоку сети

4.1 Поиск минимального пути

от источника к стоку сети в MatCad …..……………………………...…… 11

4.2 Поиск минимального пути

от источника к стоку сети в Excel …..………………………………...…… 12

5. Решение задачи о «Назначениях рабочих»

5.1 Решение задачи о

«Назначениях рабочих» в MathCad …..…...……………..…………...…… 16

5.2 Решение задачи о

«Назначениях рабочих» в Excel …..………………….…………….....…… 19

6. Вывод …..…………………………………………………..…………...…… 22

7. Список используемой литературы …..………………………...……...…… 23

8. Приложения

8.1 Приложение № 1 …..……………………………...………………….… 24

8.2 Приложение № 2 …..……………………………...………………….… 25

8.3 Приложение № 3 …..……………………………...………………….… 26

8.4 Приложение № 4 …..……………………………...………………….… 27

8.5 Приложение № 5 …..……………………………...………………….… 28

8.6 Приложение № 6 …..……………………………...………………….… 29

Условия и тексты заданий.

Сетевая задача (вариант № 25):

Задача о назначениях (вариант № 25):

Требуется назначить группу из 6 человек на 6 рабочих мест. Каждый из них может работать на любом рабочем месте, но оплата труда везде разная. Дана матрица оплаты труда. Получить оптимальное назначение с минимальными затратами на производство.

Матрица оплаты:

Краткая теория.

Понятие сетевых моделей.

Сеть – граф, состоящий из множества узлов и дуг. Каждая дуга соединяет два узла. Каждая дуга задана определенным направлением. Поэтому сеть является ориентированным графом.

Если направление дуг не задано, то говорят, что граф – неориентированный. В этом случае узлы называют вершинами, а дуги – ребрами.

Последовательность вершин и ребер, соединяющая две вершины – путь. Граф в котором можно построить путь между двумя любыми вершинами – связный граф.

В сети рассматривают ориентированные пути.

Путь который начинается и заканчивается в одном и том же узле – цикл. В сети могут быть ориентированные циклы.

Расчет максимального потока в сети.

Расчет максимального потока

в сети в MathCad.

Поток – это некая информация, передаваемая по дугам в сети.

Предположим, что эта информация имеет количественное измерение, тогда вес дуги– это пропускная способность дуги (то есть максимальное количество информации, которое можно передать по дуге), если ввести обозначение для рисунка 1:

Х_i – величина потока по i-й дуге

Рис. 1

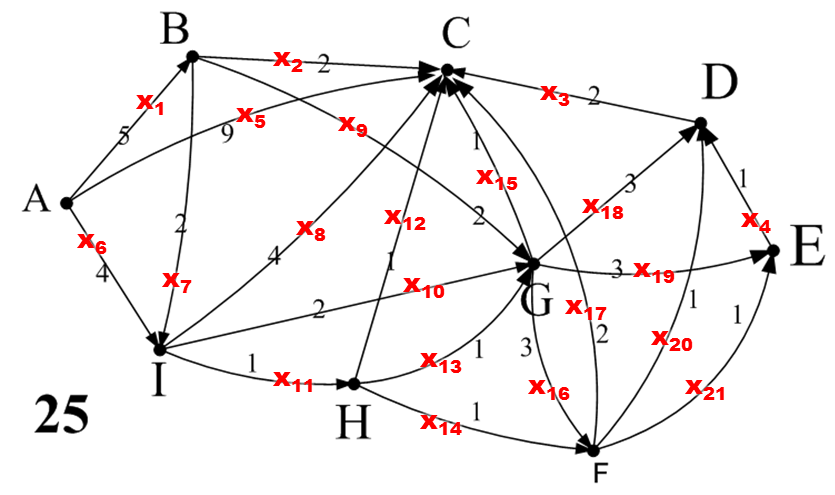
Получим ограничения пропускной способности:

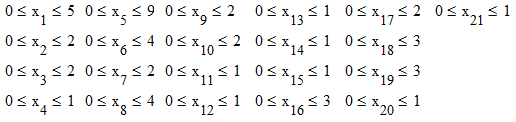
Считаем, что весь поток, входящий в узел, равен потоку, исходящему из узла.

Получим ограничения на отсутствие задержек потока в узлах:

Величину в стоке сети можно вычислить как:

, где Х – вектор потока по каждой дуге.

Получаем задачу линейной оптимизации:

Вектор решения R определяет, что по дуге х₁ необходимо пропустить поток величиной «5», по дуге x₂ – «2», по x₃ – «1» и так далее. При этом величина максимального потока = 18. Точка «А» является источником, «C» - стоком сети.

Графическая интерпретация решения (выделены дуги, переносящие максимальный поток):

Дата добавления: 2015-10-28