Краткие теоретические сведения. Нахождение корней полинома (алгебраического уравнения n-ой степени).

Нахождение корней полинома (алгебраического уравнения n-ой степени).

Цель работы:

1.Изучить принципы нахождения корней полинома с помощью встроенных функций polyroots(V) и root(f(х),х).

2.Построить графики полиномов и отобразить на них значения действительных корней.

Краткие теоретические сведения

Пусть задан полином .

Полином n -й степени с действительными или комплексными коэффициентами имеет ровно n корней действительных или комплексных. Комплексные корни могут быть только попарно сопряженными. Сразу все корни полинома можно определить, используя встроенную функцию polyroots(V), где V - вектор, составленный из коэффициентов полинома.

Вектор V состоит из n+1 элемента. Первым в векторе должен идти свободный член полинома (), вторым - коэффициент при х1() и т.д. Последним n+1- м элементом вектора должен быть коэффициент при старшей степени ().

Использование функции polyroots() не требует задания начального значения для х.

Результатом действия функции polyroots(V) является вектор, содержащий n корней полинома.

Пример №1. Найти корни полинома четвертой степени x⁴+12.5×x³+50×x²-5×x-306 с использованием функции polyroots().

Последовательность выполнения.

I. Зададим полином в виде функции F(x)

2. С помощью шаблона на панели Матрица создадим вектор vA из коэффициентов полинама:

3 Зададим имя для вектора искомых корней, например, vX. Для нахождения корней записываем оператор присваивания, в левой части которого задаем имя искомого вектора, а в правой части – функцию polyroots(vA), т.е.

4. Значения корней определяем с помощью оператора вывода:

5. Для проверки правильности найденных корней необходимо подставить полученные значения корней в полином F(x). При этом значение F(x) с заданной погрешностью должно равняться нулю. Используя оператор векторизации, можно проверить правильность сразу всех корней. Для этого в операторе вывода запишем F(vX) и применим оператор векторизации (кнопка на панели Математика)

В нашем примере получим:

С заданной погрешностью решение найдено правильно.

Коэффициенты в заданном полиноме можно определить с помощью символьного оператора coeffs на панели Символы и оператора символьного вывода.

Для этого:

1.Вставьте оператор присвоения

2.В левой части оператора напишите имя вектора, например, vV

3.В правой части введите полином.

4.На панели Символы щелкните по кнопке coeffs (Коэффициенты Полинома).

5.В маркер после вставленного ключевого слова coeffs введите аргумент полинома и нажмите клавишу Enter.

6.Справа от оператора символьного вывода появится вектор, состоящий из коэффициентов полинома.

Для нашего примера:

или проще:

II Построим график полинома в интервале, включающем найденные действительные корни. (В нашем примере два действительных корня: -4.5 и 2. Выберем интервал, в который будут попадать эти значения, например, от -5.5 до 2.5.

Задаем ранжированную переменную, например, t, которая изменяется в этом интервале с шагом 0.01.

Вставляем графическую область. Вводим аргумент t вдоль горизонтальной оси и функцию F(t) вдоль вертикальной оси. Чтобы на графике полинома в виде символов отобразить значения действительных корней, необходимо добавить вдоль горизонтальной и вертикальной осей vX и F(vX) соответственно. В окне форматирования графика на странице Оси X-Y включить опцию Показать маркеры (). На странице Графики для отметок значений корней выбрать любой символ, например, "ромб".

Ниже представлен график полинома с отображением на нем значений действительных корней в виде символа "ромб" и, проведенных в этих точках маркерных линий.

Для нахождения корней полинома n -й степени можно также использовать встроенную функцию root(). Перед вызовом этой функции следует задать начальное приближение искомого корня (действительного или комплексного). Но при каждом вызове функции root() вычисляется только один корень, поэтому для нахождения всех корней полинома n -й степени к фукции root() следует обратиться n раз. При каждом последующем обращении к этой функции необходимо исключать уже найденные корни.

Пример №2. Найти корни полинома четвертой степени F(x)=x⁴+12.5×x³+50×x²-5×x-306 с использованием функции root().

Так как корни могут быть не только действительные, но и комплексные, то нужно задать значение мнимой единицы (). В пакете Mathcad для обозначения мнимой единицы, по умолчанию, используется буква i. Можно изменить обозначение мнимой единицы с i на j.

Изменение обозначения мнимой единицы осуществляется в поле со списком Мнимое значение диалогового окна Формат результата на странице с закладкой Отображение (Параметры экрана для Mathcad 11).

Задаем значение мнимой единицы и начальное значение переменной x, например, :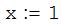

Находим первый корень и выводим его:

Для проверки подставляем значение х1 в полином F(x):

Для нахождения второго корня нужно исключить найденный корень х1. Для этого при вызове функции root() нужно разделить F(x) на (х-х1):

Для проверки подставляем значение х2в полином F(x):

Для нахождения третьего корня нужно исключить корни х1 и х2. Для этого при вызове функции root() нужно разделить F(x) на (х-х1)×(х-х2):

Проверка:

При поиске четвертого корня появится сообщение о том, что переменная х не определена.

Эта ошибка связана с тем, что вначале было задано действительное стартовое значение корня. Но т.к. предыдущий корень был комплексный, то для нахождения следующего корня нужно задать уже не действительное, а комплексное стартовое значение. Поэтому перед вызовом функции root() переприсвоим значение х. Например, зададим

Содержание отчета:

1. Номер лабораторной работы, тема и цель

2. Краткое описание использования функций polyroots() и root() для нахождения корней полиномов.

3. Условие задания, выданное преподавателем.

4. Листинг с результатами выполнения и краткими комментариями.

5. Краткие выводы.

Контрольные вопросы: 1. Сколько корней в полиноме n-й степени? 2. Может ли быть только один комплексный корень в полиноме? 3. Какая функция используется для нахождения сразу всех корней полинома? 4. Какая функция используется для нахождения одного корня полинома? 5. Что является аргументом функции polyroots()? 6. Как правильно задать вектор из коэффициентов полинома? 7.Как задать вектор из коэффициентов полинома с помощью символьного оператора coeffs? 8. Как найти корни полинома с помощью функцииroot(f(х),х)? 9. Как изменить обозначение мнимой единицы? 10. В каких случаях при поиске корней полинома нужно задавать начальное (стартовое) значение корня? 11. Каким образом исключаются найденные корни при вызове функцииroot(f(х),х)?

Дата добавления: 2015-10-28