Графический метод

Рассмотрим тот же механизм (рис. 1.29а). Разбив траекторию АВ на 8 частей (12, 24), найдем ход ползуна, начиная с крайнего положения.

Кинематические диаграммы точки С звена 3.

Кинематические диаграммы строятся методом графического дифференцирования, совмещая метод хорд и метод зеркала. Строим график перемещения S ползуна по времени.

По методу хорд находим усредненные скорости (рис. 1.30)

По методу зеркала находим скорости в точках разбиения, проведя нормаль n-n из полюса Р (рис. 1.31)

Таким же образом строим график ускорения по времени.

Если задан угол поворота φ звена, то двойным дифференцированием можно получить угловую скорость и угловое ускорение звена.

Если графоаналитическим методом можно получить скорости и ускорения всех характерных точек механизма, но для одного положения, то графический метод позволяет найти скорости и ускорения только одного звена, но для всех положений механизма.

Аналитический метод

Любой механизм может быть представлен как замкнутый векторный контур.

Дан четырехзвенник, у которого известны длины 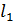, , , , и угол 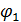, который определяет положение механизма (рис. 1.32).

Спроектируем векторное уравнение по осям X и Y:

Обозначим

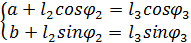(1)

Возведем каждое уравнение в квадрат и умножим их

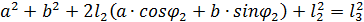
Отсюда

Обозначим правую часть уравнения через с, а отношение , тогда

Преобразуем (1)

Возведем каждое уравнение в квадрат и сложим их

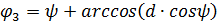
Задавая разные значения 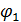, можем найти и .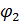

Продифференцировав уравнение (1), можем найти , .

Метод наиболее точный.

Динамика.

Динамика изучает движение материальных точек, тел и их систем с учетом действующих сил.

В динамике решаются два типа задач:

1. Дано движение тела и требуется найти силы, под действием которых это движение происходит.

2. Силы являются заданными, требуется найти закон движения.

Динамика построена на законах Ньютона.

Первый закон – изолированная материальная точка находится в состоянии покоя или равномерного и прямолинейного движения.

Второй закон – сила, действующая на материальную точку, сообщает ей ускорение, которое пропорционально величине силы и имеет направление силы

где – сила, действующая на материальную точку,

– ее ускорение,

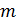– масса точки, являющаяся мерой ее инертных свойств.

Третий закон – две материальные точки взаимодействуют друг с другом так, что силы их взаимодействия равны по величине, противоположны по направлению и имеют общую линию действия.

Единица силы называется Ньютоном

Четвертый закон – если к материальной точке приложена система сил, то движение этой точки складывается из тех движений, которая точка могла бы иметь под действием каждой силы в отдельности.

Работа силы (рис. 1.33)

1. При поступательном движении

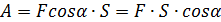
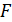Если – острый, то сила называется движущей силой, работа положительна.

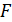Если – тупой, то сила называется силой сопротивления, работа отрицательна.

При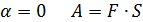

При

2. При вращательном движении тела (рис. 1.34)

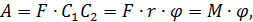
где М – крутящий момент

3. Работа силы тяжести (рис. 1.35)

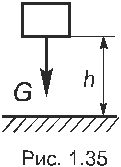
где 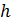– вертикальное перемещение груза.

При движении груза вверх работа считается отрицательной, а вниз – положительной, так как помогает движению.

В системе СИ сила измеряется в ньютонах, длина в метрах, поэтому за единицу работы принимается работа силы в один ньютон на пути, совпадающим с направлением силы в один метр. Эта единица работы называется джоулем.

Мощность силы

Мощностью силы называется изменение ее работы за единицу времени

Мощность, равная 1 джоулю в 1 секунду называется ваттом (Вт)

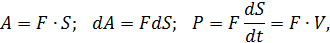
где – скорость тела.

где 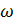– угловая скорость тела.

Кинетическая энергия для материальной точки и тела в зависимости от движения

Кинетическая энергия точки

то есть половина произведения массы 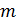точки на квадрат ее скорости.

Кинетическая энергия системы точек, то есть тела, движущегося поступательно

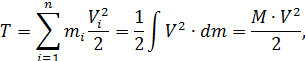
где – масса тела, .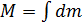

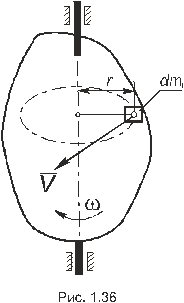
При вращательном движении (рис. 1.36)

где – момент инерции тела относительно оси Z.

При плоскопараллельном движении твердого тела

Пример: кривошипно-ползунный механизм

Метод кинетостатики (Принцип Даламбера)

Второй закон Ньютона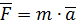

Можно записать в виде , где – сумма внешних сил и реакций связи. Введем обозначение , называется силой инерции, направлена противоположно ускорению.

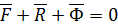
Уравнение обозначает, что в каждый момент времени движения материальной точки сумма внешних сил, реакций связей и сил инерции равна нулю.

Метод кинетостатики является формальным приемом сведения уравнения динамики к форме уравнения статики.

Дата добавления: 2015-10-28