LET'S MAKE A DEAL

This is a fine theory, but it seems to have no relation to how people actually make decisions about gambles and everything else. One simple example is Allais's paradox. Suppose you're at the final table of a poker tournament with two other entrants left. There is a $2.5 million first prize, $500,000 second prize, but no third prize. You have the middle stack, the woman on your right has 10 times your stack, and the guy on your left is down to a chip and a chair. You think there is a 10 percent chance you will win, an 89 percent chance you will take second, and a 1 percent chance you will take third. The other players offer a split. You get $500,000. The chip leader gets $2.5 million and will compensate the short stack out of that. Do you take the split?

Almost everyone says yes to this split. But now consider this situation. Same tournament and prizes, but you now have a short stack. You figure you have no chance at all to win, an 11 percent chance of picking up the $500,000, and an 89 percent chance of getting nothing. The chip leader offers to settle for second place, taking $500,000 and her chips off the table. The middle stack agrees eagerly. The only downside to you is that you think you have slightly less chance to beat the middle stack without the possibility of the chip leader taking care of him for you. With this deal, you figure to have a 90 percent chance of ending up with nothing and a 10 percent chance of winning $2.5 million. Again, everyone jumps at this split.

We've just violated the axioms of utility theory. In the first choice, we eagerly gave up a 10 percent chance to win $2.5 million to avoid a 1 percent chance of getting nothing. In the second choice, we were just as eager to get a 10 percent chance to win $2.5 million by also accepting an additional 1 percent chance of getting nothing.

The most thoughtful analysis of this paradox is in one of the great books of all time, Leonard Savage's The Foundation of Statistics. He makes a pretty good case that although everyone makes these choices, everyone is wrong, and utility theory is right. Recast the decision as a lottery with 100 tickets and the following payouts:

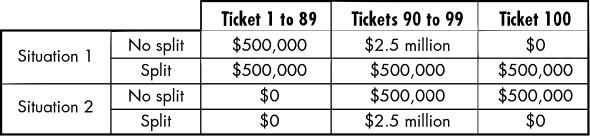
Note that this is the same as the preceding deals. In the first case, if we don't split we have an 89 percent chance to get $500,000, a 10 percent chance to get $2.5 million, and a 1 percent chance to get $0. If we split we get $500,000 in all cases. In the second situation, without a deal we get nothing 89 percent of the time and $500,000 the other 11 percent. If we split, we get nothing 90 percent of the time and $2.5 million the other 10 percent.

Savage pointed out that the decision makes no difference for tickets 1 to 89, so we should not bother considering these. For the remaining tickets, the two situations are identical, so we should make the same choice in both situations.

A curious fact about this paradox is that we are richer in situation 1. It is usually assumed that rich people have greater risk tolerance. But in Allais's paradox, the richer person turns down the gamble with the big positive expectation, while the poorer person always takes it.

So we're left with two lessons. First, people don't behave according to utility theory. Second, sometimes the theory is right. Thinking about utility theory can improve your decision making. In fact, I believe in von Neumann-Morgenstern utility theory. It's simple and elegant and gives useful predictions. When it seems to be wrong, it's usually not.

There's nothing in the theory that says gambling is irrational. That conclusion comes from restrictions people put on the theory, to make it easier to handle mathematically. A lot of people took models developed under Bernoulli's utility theory and transferred them to von Neumann-Morgenstern utility, without making use of any of the additional power and subtlety.

The key problem is that people have to make utility "time separable" to get equations that are easy to solve. Fischer Black highlighted the problem with this in his Exploring General Equilibrium. Suppose I ask you whether you would rather have $10,000 now and $100,000 in a year, or $20,000 both times. Suppose, instead, I ask if you'd rather have a coin flip-heads you get $10,000 and tails you get $100,000, or $20,000 for sure. These are entirely different questions, but time separability forces you to assume that people always give the same answer to both. Looking at things another way, the simplified theory assumes that having a 50 percent chance of something is the same as having it for half as long. For some things and some people that can be a reasonable approximation, but it is often wildly incorrect.

Дата добавления: 2015-10-26