Bluffing mathematics

To understand the mathematics of bluffing, let's go back to the game of guts and make it into a poker game. Instead of the nonsense with chips under the table and simultaneous bets, you have to either check or bet. If you check, we show hands and the better one takes the antes. If you bet, I can either call or fold. If I call, we each put in a chip, show hands, and the better hand wins four chips. If I fold, you get the antes.

Suppose you start by betting on any pair or better; otherwise, you check. You get a pair or better 49.9 percent of the time-we'll call it 50 percent to keep it simple. In the game theory analysis, you assume I know your strategy. I'm going to call your bet only if I have at least one chance in four of winning, since it costs me one chip if I lose but gains me three chips if I win. If I have a pair of sixes, I beat you one time in four, given that you have at least twos. So half the time you check, and the other half you bet. When you bet, I call you three times in eight; the tables that follow will explain why.

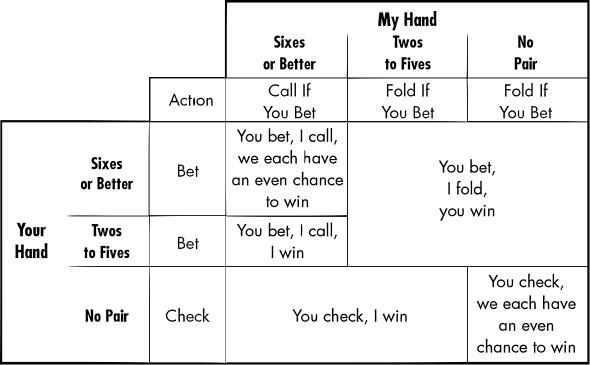
The preceding table shows the five possible outcomes. The next table shows their expected values to you. If we both have sixes or better, you bet and I call. Half the time you will win three chips, and half the time you will lose one. Your average profit is shown in the table at +1 chip. If you have any betting hand (twos or better) and I have any folding hand (fives or worse), you bet, I fold, and you win the antes, +2 to you. If you have twos to fives and I have sixes or better, you bet, I call, and I win. You lose one chip.

If you have no pair, you check. If I have twos or better, I win all the time. You get zero. If I also have no pair, you win the antes half the time, for an expected value of +1.

The following table shows the computed probabilities. We each have sixes or better 3/8 of the time, twos to fives 1/8 of the time, and no pair the other 1/2 the time. The probability of any combination is close to the product of the individual probabilities. So, for example, the probability of you having sixes or better and me having twos to fives is 3/8 x 1/8 = 3/64.

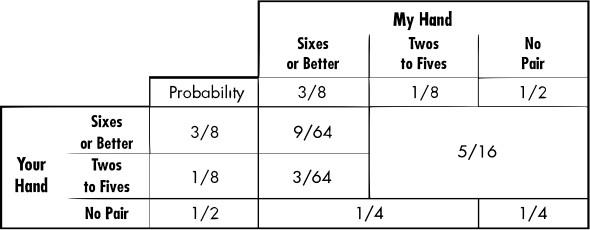
To compute your overall expected value, we multiply the numbers in the preceding two tables cell by cell, then add them up. We get +1x(9/64)+2x(5/16)-1x(3/64)+0x(1/4)+1x(1/4)=31/32. Since you have to ante one chip to play, you lose in the long run because you get back less than one chip on average.

In general, if you play your fraction p best hands, you lose p218 chips per hand. In this case, with p = %, you lose %z chip per hand. The best you can do is set p = 0. That means always check, never bet. There is never any betting; the best hand takes the antes. You will win 128 chips on average after 128 hands.

This example illustrates an ancient problem in betting. It doesn't make sense for you to offer a bet, because I will take it only if it's advantageous to me. Accepting a bet can be rational, but offering one cannot. About 200 years ago, some anonymous person discovered the lapse in this logic, which bluffing can exploit. It's possible that some people understood bluffing before this, but there is no record of it. We have plenty of writings about strategy, but none of them has the remotest hint that the author had stumbled onto this concept. Given its importance as a strategy, it's hard to believe no one would have mentioned it had it been known. Moreover, it's such an amazing and counterintuitive idea, it's even harder to believe it was so well-known that no one bothered to write about it.

The stroke of genius is to bet on your worst hands instead of your best ones. Suppose you bet on any hand queen/nine or worse, plus any hand with a pair of sixes or better. You're still betting half the time-one time in eight with queen/nine or worse and three times in eight with sixes or better. I will still call with sixes or better because I have at least one chance in four of winning with those hands.

Notice how the following outcome table has carved out a new box when you check and I have a queen/nine or worse. You move from losing these situations, with an outcome of 0, to winning with an outcome of +2. They represent 1/16 of the table, so they give you an additional expected profit of 1/8. That brings you from 31/32 to 35/32. Since that's greater than 1, you now have a profit playing this game. The trade-off is that you now lose by a lot instead of a little when you have queen/nine or worse and I have sixes or better. But that doesn't cost you any money.

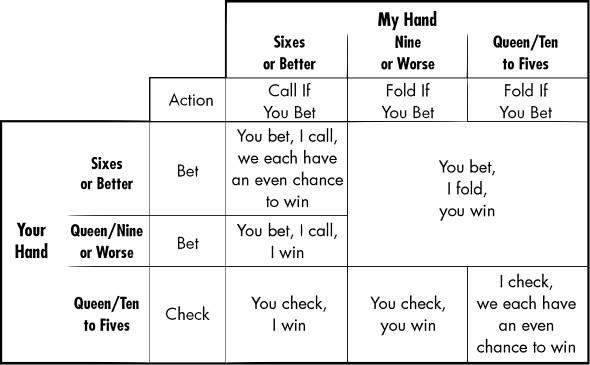
There is nothing I can do about this development. I know you're bluffing one out of four times you bet, but there's nothing I can do to take advantage of that knowledge. You're not fooling me, but you are beating me. Declaring your bet first is not a disadvantage, as it seemed at first, but an advantage-but only if you know how to bluff. Unfortunately, in real poker, other players can bluff in return and take back the advantage. Notice that it's important that you bluff with your weakest hands. This is an essential insight from game theory, which could not be explained clearly without it.

This is the classic poker bluff-acting like you have a very strong hand when you actually have the weakest possible hand. You expect to lose money when you bluff, but you more than make it up on other hands. When you have a strong hand, you're more likely to get called, because people know you might be bluffing. When you call, your hands are stronger on average, because you substituted bluffs for some of the hands you would have raised on and called on those hands instead. Bluffing doesn't depend on fooling people; in fact, it works only if people know you do it. If you can fool people, do that instead, but don't call it a bluff.

There are other deceptive plays in poker, and some people like to call these bluffs. I'm not going to argue semantics, but it's important to understand the classic bluff as a distinct idea. People are naturally deceptive, so your instincts can be a good guide about when to lie and when others are lying to you. But bluffing is completely counterintuitive; you have to train yourself to do it, and to defend yourself when others do it. Your instincts will betray you and destroy the value of the bluff; in fact, they will make it into a money-losing play. It's easy to think, "Why bluff on the weakest hands; why not use a mediocre hand instead so I have some chance of winning if I'm called?" When you get called, embarrassment might cause you to throw away your worthless hand without showing it. You may naturally pick the absolute worst times to bluff and be just as wrong about when other players might be bluffing you. Any of these things undercut the value of the bluff. Bluffing is the chief reason that people who are good at other card games find themselves big losers in poker to average players.

The classic bluff amounts to pretending to be strong when you are weak. Pretending to be weak when you are strong, also known as slowplaying, is a standard deception strategy type. I prefer not to call it a bluff. The classic bluff is to raise on a hand you would normally fold; slowplaying is calling on a hand you would normally raise. The bluff goes from one extreme to the other; slowplaying goes from one extreme to the middle. You should always mix up your poker playing, but unless you're bluffing, you move only one notch: from fold to call or call to raise or vice versa. You would never bluff by folding a hand you should raise-that would be crazy. Another distinction is that you slowplay to make more money on the hand in play; you bluff expecting to lose money on average on the hand, but to increase your expectation on future hands.

A more interesting case is the semibluff. This is one of the few important concepts of poker clearly invented by one person: David Sklansky. I don't mean that no one ever used it before Sklansky wrote about it. I have no way of knowing that. But he was the first to write about it, and he had the idea fully worked out. You semibluff by raising on a hand that's probably bad but has some chance of being very good.

An example is the six and seven of spades in hold 'em. If the board contains three spades, or three cards that form a straight with the six and seven, or two or more sixes and sevens, your hand is strong. Even better, other players will misguess your hand. Your early raise will mark you for a pair or high cards. Suppose, for example, the board contains a pair of sevens, a six, and no ace. If you bet strongly, people will suspect that you started with ace/seven, and play you for three of a kind. Someone with a straight or flush will bet with confidence. You, in fact, have a full house and will beat their hand. Or if the board comes out with some high cards and three spades, people will think you have paired your presumed high cards or gotten three of a kind. You actually have a flush.

I prefer to think of raising with this hand preflop as a randomized bluff. When you make the raise, you don't know whether you're bluffing. I don't like the term semiblu f f because it implies that you're sort of bluffing. You're not. You're either bluffing or you're not-you just don't know which yet. That's an important distinction. Sort of bluffing never works; randomized bluffing can work. Sklansky states that you should expect to make money on your semibluffs-in fact, on all bluffs. To my thinking, if you expect to make money on the hand, it's deception, not bluffing. When you bet for positive expected value, it's no bluff. You may have a weak hand that will win only if the other player folds, but if the odds of her folding are high enough, your play is a lie, not a bluff.

Given Sklansky's refusal to make a negative expected value play, a randomized bluff is the only way to incorporate bluffing into his game. The disadvantage of semibluffs is that you lose control over when you bluff. You need a certain kind of hand for it, so you could go an hour or more without getting one-and even if you get it, it might not turn into a bluff. If you practice classic bluffing, the deal is unlikely to go around the table without giving you some good opportunities. You even have the luxury of choosing your position and which player to bluff, or bluffing after a certain kind of pot.

Semibluffing makes the most sense when two conditions are met. First, the game might not last long enough for you to collect on the investment of a bluff with negative expectation. The extreme case of this is when the winner of a large pot is likely to quit the game. This happens a lot online. Players don't even have to leave physically: If they tighten up enough, they might as well be gone. Second, the bluff is aimed at turning a break-even or better situation into a more profitable one, rather than a money-losing situation into break-even or better. For improving a break-even situation, you can afford to wait as long as it takes for the right bluff. If you're working a losing situation, you should bluff soon or quit the game.

GAME FACT

A game theory analysis of bluffing is just one way of looking at one aspect of poker. Game theory teaches many valuable lessons, but overreliance on it has led to some absurd weaknesses in the standard way the modern game is played.

For one thing, game theory teaches that there is no advantage to concealing your strategy, only your cards. Players are taught to watch intently when other players first pick up their cards and to take great pains to disguise any of their own reactions. Those same players will chatter openly about their playing strategies. "I hate playing small pairs," they'll announce to the world, or "suited jack/ten is the best pocket holding."

Not all of this information is true. The guy who hates small pairs probably does so because he plays too many of them. A guy who swears he'll never touch another drop of alcohol is likely to put away more liquor in the next year than the guy who doesn't talk about his drinking. But rarely in my experience is this talk deliberate misdirection. The important thing is that it tells you how the player thinks about the game. Listen when people tell you stories about their triumphs and frustrations-they're telling you how they play and what matters most to them. Do they crow about successful bluffs or when their great hand beat a good hand? Do they gripe about people who play bad cards and get lucky or people who play only the strongest hands? Of course, the answer in many cases is both, but you can still pick up some nuances. I don't know whether to be more amazed that players give this kind of information away for free or that other players don't pay attention to it. I learned a more traditional version of poker, in which you have to pay to learn about someone's strategy.

You will learn a lot more useful things studying players before they pick up their hands than after. For one thing, game theory has put them off guard during the shuffle and deal. There's less misdirection and less camouflage. For another, it's hard to learn much that's useful about someone's cards, unless they're wearing reflector sunglasses. You might get a general impression that the hand is pretty good or bad, but you'll figure that out soon enough from the betting. It's hard to read the difference between suited ace/nine and a pair of eights. A really bad player will tip off what he thinks the strength of his hand is, but a really bad player is often mistaken. You can't read in his face what he doesn't know. A really good player is at least as likely to be telling you what she wants you to think, rather than giving away useful information. Anyway, poker decisions rarely come down to small differences in other players' hand strengths. Determining the winner will come down to those small differences, but the way you play the hand doesn't.

However, knowing someone's strategy tells you exactly how to play them. It's often possible to see in someone's manner before the deal that he's going to take any playable hand to the river or that he's looking for an excuse to fold. One guy is patiently waiting for a top hand, smug behind his big pile of chips. Another is desperate for some action to recoup his losses. Knowing this will help you interpret their subsequent bets and tell you how to respond.

If you know their strategies, you don't need to know their cards. Say you decide the dealer has made up his mind to steal the blinds before the cards are dealt. As you expect, he raises. You have only a moderate hand, but you call because you think he was planning to raise on anything. If he turns out to have a good hand by luck, you will probably lose. But you don't care much, since on average you'll win with your knowledge. Knowing his cards would only help you win his money faster-too fast. People will stop playing if every time you put money in the pot, you win. If you did know everyone's cards, you would lose on purpose once in a while to disguise that fact. In the long run, everyone's cards are close to the expected distribution, so you don't have to guess.

The game-theoretic emphasis on secrecy spilled over into cold war diplomacy. A cold war thriller is, almost by definition, an espionage story (usually with the possibility of the world being destroyed if the good guys lose). The obsession with spies looks pretty silly today because almost all major security breaches were by spies selling out their own countries. We would have had far better security with less obsession about spying and counterspying. If you let foreign agents loose among all government documents, they can spend eternity trying to winnow out the few items that are both valuable and accurate. When you segregate all the important stuff in top secret folders, you do your enemies a favor. You double that favor by creating such a huge bureaucracy to manage the secrets that it's a statistical certainty you're hiring some traitors or idiots.

On top of that, making essential public data secret undercuts both freedom of the press and the people's right to choose. When the party in power and entrenched public employees get to decide what's secret, it's even worse. The joke, of course, is that all the cold war disasters were disasters of strategy. It wasn't that either side didn't have good enough cards, it was that they played them foolishly. All the financial and human resources wasted on getting better cards (that is, building more terrible weapons) supported a strategy of risking everything and terrifying everyone, for nothing.

Getting back to poker, another reason for focusing on strategy rather than cards is that you cannot change someone's cards (legally, anyway), but it's easy to change their strategy. Consider the original game of guts discussed previously, in which both players declare at the same time. If the other player follows the game-theoretic optimum strategy of playing the strongest half of his hands, ace/king/queen/jack/two or higher, there's no way for you to win. But if he deviates in either direction, playing more or fewer hands, you can gain an advantage.

If he plays fewer than half his hands, your best strategy is to play all of yours. If he plays more than half his hands, your best strategy is also to play loose, but only half as loose as he does. For example, if he plays 70 percent of his hands, you play 60 percent (half the distance from 50 percent). If he plays exactly half his hands, it doesn't matter whether you play anything from 50 percent to 100 percent of yours. This general result applies to many game situations. If another player is too tight, even a little bit, you respond by being very loose. If another player is too loose, you want to be about half as loose. Another general result suggests that you try to make a tight player tighter and a loose player looser. You want to drive other players away from the optimal strategy, and it's easier and more profitable to move them in the direction they want to go anyway.

To a game theorist, this information is irrelevant. You play assuming your opponent does the worst possible thing for you, so you don't care what he actually does. But I do care what he actually does. My guess is that most poker players are going to start out too tight, since they've been trained to wait for good hands. That means I start out playing all my hands. I'll probably make money that way. At worst, I'll have a small negative expectation. If so, I'll find it out very soon, the first time a player bets with a weak hand.

Of course, my playing all my hands and his losing money steadily will encourage him to loosen up. I can judge the degree of looseness very precisely because I see all the hands he bets on. That's another reason to start out loose: I want to learn his strategy. Game theory does not value that, because it starts by assuming that everyone knows everyone else's strategy. Once he loosens up enough to play 50 percent of his hands, I want to pull him looser quickly. As in judo, the trick is to use the other person's momentum against him.

How do I do that? I bet blind. Instead of looking at my hand and squirreling a chip under the table, I pick up a chip and put it in my fist above the table. I don't say anything; I just do it. Betting blind (when it's not required) is an important ploy in poker to change other players' strategies, but it has disappeared from modern books because game theory says it is never correct to ignore information.

If I do things right, I can get him playing much more than 50 percent of his hands. To take advantage of that, I have to play half as loose as he does. That will take some close figuring, but I can do it for a while. When he gets tired of losing showdowns, he'll start to tighten up, and I'll go back to playing all my hands.

Of course, he could be trying to do the same things to me. If he stays one step ahead, or gets me playing by emotion instead of logic, or just keeps me off balance, he's going to win. One of us will win and one will lose, and the luck of the cards has nothing to do with it. There's no neat mathematical way to decide who will win, and there's no way to calculate the risk. That's the essential nature of games-good games, anyway-and it's entirely missing from game theory. Everyone was born knowing this; it took mathematics to confuse people. If you keep your common sense, play a clear strategy, and encourage other players to play a strategy you can beat, you won't find many people playing at your level.

This example reveals another defect of game theory. The optimal strategy often means that all opponents' strategies work equally well. The game-theoretic strategy for Rock Paper Scissors, for example, is to play each shape at random with equal probability. If you do this, you will win exactly half the games in the long run (actually, you win one-third and tie one-third, but if ties count as half a win, that comes out to winning half the time). You win one-half, no more and no less, if I always play rock, or always play what would have won last time, or always play the shape you played last time. You can't lose, but you also can't win. That's not playing at all. If you want to avoid the game, why waste the effort to pretend to play?

It makes more sense to adopt a strategy that gives other players many opportunities to make costly mistakes rather than one that gives you the same return no matter how they play. Instead of starting from the idea that everyone knows everyone's strategy and plays perfectly given that knowledge, let's make the more reasonable assumption that there is uncertainty about strategies and imperfect play. Now winning comes down to making fewer mistakes than other players. You can accomplish that by reducing your own mistakes or increasing theirs.

If you're the better player, the first course is difficult because you're already good. But the second course is easy: As the better player, you should be able to manipulate the table and keep everyone else off balance. If you are equally as good as the other players, it still makes sense to try the second approach. If you avoid one mistake, that's one mistake in your favor. But if you induce a mistake in other players' play against you, that's one mistake per player in your favor. Only if you are the worst player does it make more sense to improve your own play than to try to disrupt others. In that case, the game theory approach is a good defense. But, as I've said before, an even better approach is to quit the game until you're good enough to compete.

Дата добавления: 2015-10-26