П.2. Отчет по лабораторной работе

«Измерение плотности прямоугольного параллелепипеда»

Цель работы: ознакомиться с методикой обработки результатов прямых и

косвенных измерений физических величин; измерить плотность твердого тела.

Приборы и принадлежности: штангенциркуль, весы лабораторные.

Эскиз тела:

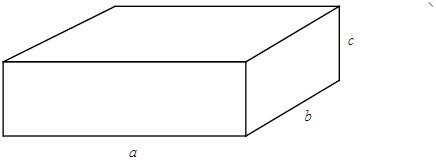
Уравнение измерения:

, (1)

где 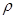- плотность, - масса, 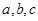- линейные размеры тела.

Результаты измерений:

№ изм.	,мм	,мм	,мм	,г
	38,9	29,4	17,5	160,3
	39,0	30,1	17,4	160,3
	39,1	29,9	17,5	160,3

Вычисление наилучших значений линейных размеров:

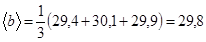мм, 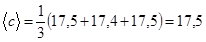мм,

мм.

Вычисление абсолютных погрешностей:

мм, аналогично находим , мм;

мм, аналогично находим мм, мм;

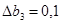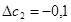, аналогично находим мм, .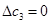

Вычисление средней абсолютной погрешности линейных размеров:

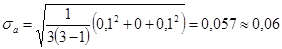мм; поскольку 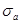больше инструментальной погрешности штангенциркуля (0,05 мм), 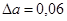мм;

мм; поскольку 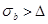, мм;

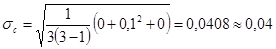мм; поскольку , 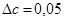мм.

Учитывая, что масса тела предполагается известной, считаем, что Вычисление наилучшего значения плотности тела:

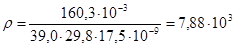кг/м³.

Для вычисления относительной погрешности плотности необходимо найти частные производные по переменным уравнения измерения (1), прологарифмированного по натуральному основанию:

.

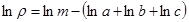Частные производные находятся по тем же правилам, которые используются при дифференцировании функций одной переменной. Например, вычисляя частную производную 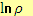по переменной , остальные переменные полагаем константами и находим:

.

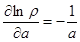Аналогично имеем:

, , .

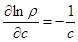В соответствии с этим получим формулу для вычисления относительной погрешности:

.

В результате подстановки численных значений имеем (с учетом правил приближенных вычислений):

что составляет 0,7%.

Вычисляем среднюю абсолютную погрешность:

кг/м³.

Таким образом,

кг/м³, .

Вывод: изучили методику обработки результатов прямых и косвенных измерений, измерили плотность твердого тела, имеющего форму прямоугольного параллелепипеда.

Дата добавления: 2015-10-26