
Читайте также:
|
Обертальний електромагнітний момент М ем двигуна виникає в результаті взаємодії магнітного поля ротора, яке створюється струмом I 2 обмотки ротора, із обертовим магнітним полем статора. У загальному випадку його визначають за формулою:

де с – коефіцієнт, величина якого визначається конструктивними особливостями машини; Ф1 – магнітний потік полюса поля статора, яке обертається; j2 – кут зсуву фаз між струмом і ЕРС роторної обмотки.
Як було показано у розділі “Магнітні кола” і далі у розділі “Трансформатори”, величина магнітного потоку є пропорційною напрузі струму, який створює цей потік. Таке справедливо і для АД, тобто, Ф1 º U 1. Оскільки I 2cosy2 º E 2 s º Ф1 º U 1, то звідси випливає дуже важливий для АД висновок – обертальний момент є пропорційним квадрату напруги, підведеної до статорних обмоток двигуна:
 .
.
Велике теоретичне та практичне значення має залежність обертального електромагнітного моменту М ем від ковзання s, яку називають механічною характеристикою (рис.4.7).


Аналітичний вираз залежності М ем= f (s) –
 ,
,
можна отримати шляхом підстановки у формулу розрахунку М ем виразів I 2 та cosj2 через s, які наведені у попередньому розділі. Якісний вигляд механічної характеристики АД загального призначення показаний на рис. 4.7.
Оскільки механічна характеристика відображає фізичні процеси, які відбуваються в АД, то її часто використовують для аналізу експлуатаційних можливостей двигуна.
Так, в момент пуску двигуна, ковзання має максимальне значення s п= 1, внаслідок чого E 2 s, I 2, xL 2 максимальні, а j2» 90°.
Максимальному струму ротора I 2 відповідає максимальне – пускове, значення струму I 1п, який статорні обмотки двигуна споживають від трифазного джерела напруги. Досвід експлуатації АД свідчить, що в момент пуску I 1п = (5…8) I 1н. Це призводить до значного виділення теплоти в обмотках і, отже, може призвести до їх пошкодження. Звідси випливає, що пуск АД доцільніше здійснювати при відсутності навантаження на валу двигуна, тобто на холостому ході.
Не дивлячись на те, що АД має великий пусковий струм, пусковий електромагнітний момент М п у двигуна відносно малий. Це пояснюється тим, що cosj2» 0. Звідси також випливає, що АД доцільно запускати у холостому режимі. При пуску без навантаження гальмівний момент двигуна значно менший ніж пусковий і номінальний М н, тому ротор швидко починає набирати оберти.
Зі збільшенням обертів n 2 ротора, тобто при зменшенні ковзання, зменшуються E 2 s, I 2, xL 2, але збільшується cosj2 двигуна. Це призводить до збільшення електромагнітного моменту до максимального значення М max. Наявність екстремуму у кривій М ем(s) означає, що гальмівний момент на валу АД можна збільшувати тільки до певної межі, далі якої двигун зупиниться.
Значення ковзання, яке відповідає М max, називають критичним s кр, в зв’язку з чим і максимальний обертальний момент АД також інколи називають критичним. Відмітимо, що М ем = М max, коли j2 = 45°, а xL 2= r 2. Остання з ознак, як буде показано далі, використовується при керуванні двигуном з фазним ротором.
При подальшому збільшенні обертів ротора до максимально можливих – обертів холостого ходу n 20, тобто зменшені ковзання до мінімально можливого значення s 0, внаслідок різкого зменшення I 2, обертовий момент швидко зменшується до М 0.
Величина ковзання s і частота обертання ротору n 2 зв’язані між собою через постійну (n 1 = const) для конкретного двигуна величину –
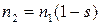 .
.


При обертанні ротора з постійною частотою, в межах n 20 < n 2 < n 2кр, момент опору на валу двигуна складається з моменту холостого ходу та статичного моменту навантаження з боку робочої машини і дорівнює М ем. Це дає підстави надати механічну характеристику АД у вигляді більш зручному для аналізу роботи електроприводу – у координатах: частота обертання ротора n 2 від моменту на валу двигуна M (рис. 4.8).
З рис. 4.8 видно, що в режимі холостого ходу, коли момент опору на валу обумовлений втратами у двигуні (М = М 0), ротор обертається з максимальною частотою n 20 – максимально близькою до частоти обертання поля статора (синхронної частоти). Із збільшенням моменту опору до номінального М н і далі до М max, наприклад за рахунок гальмуючого моменту з боку робочої машини, частота обертання ротора зменшується до номінальної n 2н і далі до критичної n 2кр. При подальшому збільшенні моменту опору (при М > М max) n 2 швидко зменшується до нуля (двигун перекидається – сленг, тому М max інколи називають критичним або перекидаючим моментом) і двигун потрапляє у пусковий режим, де, нагадаємо, I 1п = (5...8) I 1н. Якщо при цьому статорні обмотки не відключити від мережі живлення, то вони згорять.
Оскільки у разі зменшення моменту опору від М max до М 0 маємо зворотне – частота обертання ротору збільшується до n 20, то цю частину характеристики між точками з координатами (М 0, n 20) та (М кр, n 2кр)називають зоною стійкої роботи двигуна, або робочою ділянкою. Ділянку характеристики між точками з координатами (М кр, n 2кр) та (М п, 0) називають зоною нестійкої роботи двигуна.
В теорії електроприводу за величиною D n 2 = n 20 - n 2н робочі ділянки двигунів поділяють на: абсолютно жорсткі (D n 2 = 0), жорсткі (D n 2 £ 0,2 n 2н– мала величина, яка не має суттєвого впливу на роботу електроприводу і керування ним) та м’які (D n 2 > 0,2 n 2н– значна величина, яка має суттєвий вплив на роботу електроприводу і керування ним).
У АД з КЗР загального призначення D n 2 £ 0,2 n 2н, отже ці двигуни мають жорстку робочу ділянку механічної характеристики. Разом з тим, механічні характеристики, а також їх робочі ділянки, АД з КЗР спеціального призначення можуть мати якісно інший вигляд. Для порівняння на рис. 4.9 показані механічні характеристики АД з КЗР: загального призначення 1, з підвищеним пусковим моментом 2, з підвищеним ковзанням 3, кранових 4.


На практиці, робочу ділянку механічної характеристики АД розраховують за більш простою формулою Клосса:

 ,
,
де Mk і sk – поточні значення, відповідно, моменту на валу двигуна і ковзання.
Робочі характеристики АД являють собою залежності частоти обертання ротора n 2 (швидкісна характеристика), коефіцієнта потужності cosj1, величини струму у статорних обмотках I 1 і корисного моменту на валу –
|
 ,
,
від корисної потужності P 2 двигуна при U 1 = const та f 1 = const. Їх якісний вигляд для АД загального призначення показаний на рис. 4.10.
Дата добавления: 2015-10-24; просмотров: 197 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Втрати потужності і коефіцієнт корисної дії асинхронного двигуна. | | | Приклад спрощеного розрахунку механічної характеристики асинхронного двигуна. |