А.4 Кинетика периодической адсорбции

Периодическая адсорбция является нестационарным процессом массообмена между потоком разделяемой газовой смеси, содержащей поглощаемый компонент (адсорбтив), и неподвижным слоем адсорбента. В общем случае этот процесс характеризуется последовательным массопереносом адсорбтива из ядра потока к поверхности частиц адсорбента (внешний массоперенос) и от этой поверхности - внутрь частиц (внутренний массоперенос). В отдельных случаях процесс может лимитироваться либо внешним, либо внутренним массопереносом.

Расчет адсорберов периодического действия основывают на закономерности изменения во времени степени насыщения адсорбента и концентрации адсорбтива в газовой фазе в каждом сечении слоя адсорбента. Это пространственно - временное распределение поглощаемого компонента между фазами можно представить следующим образом. При входе газового потока с постоянной начальной концентрацией адсорбтива 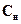(кг/м3) в слой свежего адсорбента с концентрацией поглощаемого компонента (адсорбата) а=0 адсорбируемый компонент начинает поглощаться первым рядом гранул адсорбента, затем вторым, третьим и т.д. С течением времени вовлекается в работу много последовательно расположенных рядов частиц адсорбента, однако, каждый последующий ряд омывается потоком газа с концентрацией адсорбтива 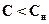, так как часть его уже поглощена предыдущими рядами.

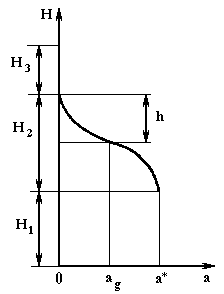Рис. А.3. Кривая распределения концентрации адсорбата по высоте слоя адсорбента

После предельного насыщения частицы первого ряда выключаются из процесса поглощения, и газ с концентрацией 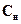начинает омывать частицы второго ряда, затем третьего и т.д. Таким образом, с течением времени по высоте слоя адсорбента Н образуются три зоны (рис. А.3): 1 - зона отработанного адсорбента (высота Н1), где достигнута предельная емкость (концентрация) а^* (т.е. находящаяся в равновесии с газовым потоком концентрации 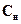); 2 - работающая зона (высота Н2), где предельная емкость еще не достигнута, и процесс адсорбции продолжается; 3 - зона не включенного еще в работу адсорбента (высота Н3). Насыщение первого ряда частиц адсор-бента происходит с падающей скорос-

тью, так как по мере приближения к предельному значению а^* непрерывно уменьшается движущая сила процесса.

Математическая модель процесса периодической адсорбции может быть представлена в виде следующей системы уравнений в предположении о движении газовой фазы, соответствующем идеальному вытеснению

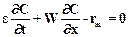(А.3)

(А.4)

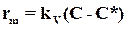(А.5)

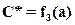, (А.6)

где 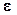- порозность зернистого слоя адсорбента, W –фиктивная скорость движения газа в слое, r_m – источник (сток) массы, обусловленный переносом адсорбтива из газовой фазы в твердую, k_V – объемный коэффициент массопередачи, 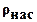- насыпная плотность адсорбента. Система дифференциальных уравнений с частными производными должна быть дополнена соответствующими начальными и граничными условиями. Обычно предполагается, что начальная концентрация адсорбата равна нулю или некоторой остаточной после регенерации величине а_о, а граничная концентрация абсорбтива в газовой фазе С_н.

Анализ решения системы уравнений (А.3) - (А.6) показывает, что для выпуклой изотермы адсорбции (А.2) рис. А.1 и постоянного значения коэффициента массопередачи k_V втечение определенного времени происходит формирование стационарного профиля концентрации С (х) – фронта адсорбции, а затем осуществляется его параллельный перенос с постоянной скоростью 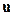(рис.А.4). Для линейной и тем более вогнутой изотерм адсорбции профиль концентрации С(х, t) с течением времени все более расширяется, что не позволяет говорить в этих случаях о параллельном переносе стационарного фронта адсорбции.

Для расчета и анализа работы адсорберов периодического действия используется понятие времени проскока t_пр (времени защитного действия слоя), соответствующее времени работы адсорбера при котором концентрация адсорбтива на выходе из слоя адсорбента станет равной некоторой заданной максимально допустимой проскоковой концентрации С_пр, по достижении которой следует процесс прекращать и производить регенерацию адсорбента. Оно может быть найдено решением системы уравнений (А.3)-(А.6) при С (Н, t_пр)=С_пр, которое получается аналитически либо численными методами в зависимости от вида изотермы адсорбции.

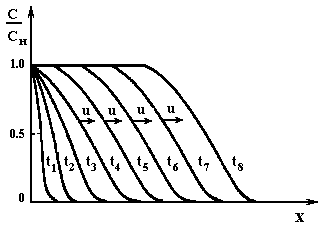Рис. А.4. Профили концентраций адсорбтива С(х,t)при прохождении слоя адсорбента

Средняя концентрация адсорбата в слое при проскоке 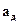называется динамической активностью или емкостью адсорбента (рис. А.3), причем 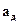<а^* вследствие того, что концентрация адсорбата в конечных слоях адсорбента меньше равновесной. Получить максимальное значение вре-мени проскока можно вос-пользовавшись моделью идеа-льной равновесной адсорбции, в соответствии с которой пред-полагается бесконечно большая скорость массопередачи (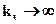) и предельно выпуклая

(ступенчатая) изотерма адсорбции. В этом случае каждый элементарный слой адсорбента будет насыщаться адсорбатом до равновесного значения а^*(С_н) и лишь затем включаться в работу следующий слой. Проскок наступит лишь тогда, когда весь адсорбент насытиться адсорбатом до а^*(С_н).

Время проскока можно определить из уравнения материального баланса, приравняв количество адсорбитва, ушедшего из газовой фазы за время t, количеству адсорбата, поглощенного адсорбентом

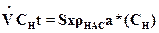, (А.7)

где 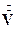- объемный расход газа, S – площадь поперечного сечения слоя адсорбента. Учитывая, что 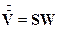, перепишем (А.7) в виде

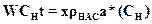(А.8)

Время проскока для модели идеальной адсорбции t_{пр.ид .} будет соответствовать насыщению всего слоя адсорбента высотой Н

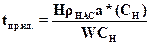(А.9)

Действительное время проскока будет меньше идеального, и для его нахождения используют вместо статической активности (равновесной концентрации адсорбата) динамическую активность

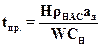(А.10)

либо вводят величину потери времени защитного действия слоя t_о, обусловленную конечной скоростью массопередачи

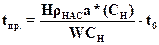(А.11)

Последнее уравнение носит название уравнения Шилова.

Из уравнения материального баланса можно получить и величину скорости параллельного переноса фронта адсорбции u. Запишем его для системы отсчета, перемещающейся с фронтом адсорбции

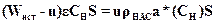(А.12)

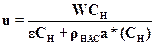(А.13)

где W_ист – истинная скорость движения газового потока в слое адсорбента. Такое же решение для u получается и из системы уравнений (А.3) – (А.6).

Дата добавления: 2015-10-24