Метод карт Карно

Карта Карно – це графічний засіб для спрощення логічних рівнянь або перетворення таблиць істинності у відповідну логічну схему простим і впорядкованим шляхом.

Як і таблиця істинності, карта Карно є засобом, що показує співвідношення між логічними входами і необхідним виходом.

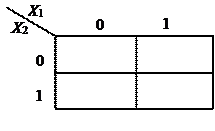Особливість карти Карно полягає в тому, що по горизонталі та по вертикалі задаються координати клітин, якими виступають аргументи логічної функції. Тому кожна клітина має свою координату – 00, 01, 11, 10, яка може бути представлена відповідною двійковою або десятковою цифрою. Значення функції записується в відповідних клітинах нулями та одиницями. Наприклад, для двох змінних карта Карно має вигляд:

умова Х ₁ = 0, Х ₂ = 0 відповідає лівому верхньому кутку, а Х ₁ = 1, Х ₂ = 1 – правому нижньому кутку.

Для трьох вхідних змінних карта Карно має вигляд:

При переході від однієї комірки до сусідньої змінюється лише одна змінна (00, 01, 11, 10).

Для чотирьох вхідних змінних карта має вигляд:

Наприклад, задана таблиця 2.8 чотирьох змінних.

Таблиця 2.8

X 4	X 3	X 2	X 1	Y

Спосіб мінімізації логічних виразів спрощується тим, що клітинки, які відрізняються тільки по одній змінній, можна об'єднати. Наприклад, в двох членах тільки змінна X₃ міняє свій стан з прямого на інверсний, а X ₁та X ₂залишаються незмінними. Ці два члени можуть бути згруповані (суміщені) таким чином, що в результаті змінну Х ₃можна скоротити, оскільки вона з'являється як у нормальному стані, так і в інверсному.

Відповідно до табл. 2.8 складаємо карту Карно наступним чином, при цьому X ₂ X ₁ – визначає стовпчик, X ₄ X ₃ – визначає рядок. Відповідно одиницю ставимо у верхній крайній куток.

Складемо логічні вирази всіх вхідних змінних для кожної комірки, де знаходиться одиниця. У групі А отримаємо кон'юнкцію:

Для групи В отримаємо кон'юнкцію:

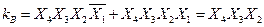
У одну групу також зв'язують ті комірки, які знаходяться в лівому і правому краях одного рядка або у верхній і нижній частинах одного стовпчика. Так карти Карно дозволяють проводити мінімізацію не виконуючи перетворення, а шляхом записування однакових символів Х для всієї групи. Для групи С отримаємо кон'юнкцію:

У логічній сумі всіх отриманих виразів маємо:

.

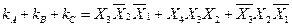Дата добавления: 2015-10-24