Математическое моделирование в системном анализе

Моделирование и модели

Небольшое отступление. Вспомним, что исследователь в частных науках, технике – специалист. Исследователь в системной науке, практике – генералист (но, увы, не всегда генерал). Генералист, системщик обязан быть широко мыслящим человеком, эрудитом. Например, хороший менеджер – это системный практик.

«Специалист – это человек, который узнаёт всё больше о всё меньшем и в пределе знает абсолютно всё абсолютно ни о чём. Эрудит – человек, который узнаёт всё меньше о всё большем и в пределе узнаёт абсолютно ничего абсолютно обо всём» (фольклор). Ни к одному из этих пределов стремиться не нужно. Оптимум – где-то посредине. Но в сложном, взаимозависимом и быстро меняющемся мире любой специалист обязан быть эрудированным человеком и хоть немного – генералистом. Особенно специалист в такой развивающейся сфере, как информатика, информационные технологии. Изучение системной науки очень этому способствует. Тем более что она как ни одна другая объединяет точные методы с гуманитарными, математику с психологией, технику с человеком и организацией.

Теперь к методам изучения. Несмотря на, казалось бы, огромное разнообразие систем существуют некие общие подходы к их изучению. Главным методом изучения систем является моделирование, разработка моделей. Вообще моделирование – это единственный рациональный (основанный на разуме) метод познания действительности. Существуют ещё интуиция, озарение (инсайт) и т.п., но это не в тему курса.

Моделирование - это построение и изучение структурных, логических, математических и других абстрактных моделей систем и процессов в них. Системы – как уже существующие, так и разрабатываемые. Есть ещё и физическое моделирование, но оно используется в частных науках и в технике (уменьшенные копии, модели самолётов, кораблей, зданий, мостов для экспериментов), но не в системных исследованиях.

О видах моделях и методах моделирования.

Определение 9. Модель – это отображение существенных свойств объекта (системы) при его изучении.

Основным методом изучения систем является математическое моделирование. А основным инструментом исследования математических моделей сложных систем является компьютер. Только для некоторых очень простых математических моделей систем могут быть получены аналитические (в виде формул) решения. Математические модели представляют собой системы уравнений (чаще всего – дифференциальных уравнений) и ограничений (в виде равенств и неравенств). Эти системы разрабатываются исходя из базовых «законов природы» и конкретных теорий в данной предметной области. В общем, для построения хороших математических моделей надо знать предметную область, нужные разделы математики и применять системный подход. Такие модели называют физичными, системными, или моделями «прозрачного ящика». Они – основные в технике. Например: модель процесса выведения спутника на орбиту, или модель работы прокатного стана. Применяются и в экономике предприятия (модели «индустриальной динамики») и в мировой экономике (модели «глобальной динамики» Римского клуба), и в экологии (модель «ядерной зимы»), и во многих других областях. Эти модели очень трудоёмки и для них критически важна проблема надёжных исходных данных. Но это – главное направление моделирования в эпоху компьютеров.

Для многих сложных систем по разным причинам трудно (или не нужно) построить хорошую физичную модель. Пример: экологические, экономические, социальные системы. Известны входы и выходы системы и имеется много данных о её «работе». Это – так называемая модель «чёрного ящика», или кибернетическая модель. Если здесь можно применить методы математической статистики и теории вероятностей, то это - статистический метод моделирования, прикладной статистический анализ. А модели, конечно, называются статистическими. Например, модели систем массового обслуживания (они моделируют процессы получения и обработки заявок, поступающих случайным образом на входы системы).

Примеры систем массового обслуживания?

Частным видом математических моделей всех видов являются оптимизационные модели, о них говорилось выше.

Соединение физичных моделей сложных систем со статистическими методами формирования наборов исходных данных и обработки результатов называется имитационным моделированием, а сами модели – имитационными.

Исследование поведения систем при помощи имитационных математических моделей и компьютеров называется вычислительным экспериментом.

В системном анализе ключевую роль играют системно-структурные или просто структурные модели, представляющие проблему в виде системы с определенной структурой. При построении их используется теория графов. С ними мы познакомимся в разделе, посвященном методам многокритериального анализа. Пока отметим, что структурные модели могут при необходимости дополняться любыми другими.

Наконец, в системном анализе важную роль играет вербальная (словесная) аналитика – рациональное, логичное описание системы и процессов в ней на естественном языке. В системном исследовании не обойтись без экспертных суждений и неформальных процедур. Это – так называемый информационно-аналитический метод. Для гуманитариев – это основной метод. Во второй части курса мы рассмотрим вербальный анализ решений.

Теперь о требованиях к математическим моделям.

1. Замкнутость. Смысл этого требования прост: модель должна работать, т.е. после ввода исходных данных она должна выдать правдоподобный результат.

2. Адекватность. Свойств у объекта очень много и все их в модели не отразить. Да это и не надо. Свойства, важные для целей исследования, называются существенными. Модель, правильно учитывающая все существенные (для данной задачи!) свойства и, поэтому, дающая достаточно правильные (для данной задачи!) ответы называется адекватной. Критерий правильности – практика.Для каждой модели существует своя область применимости – такой набор задач и диапазон исходных данных, где она даёт правильные ответы и поэтому является адекватной. А вне области?Определение границ области применимости моделей сложных систем – нетривиальная задача. Но о границах применимости модели (любой и любого вида – вербальной, математической, статистической, системно-структурной) забывать нельзя.

3. Релевантность. Модель должна соответствовать современному уровню знаний в моделируемой предметной области.

4. Эффективность. Модель должна быть эффективной, то есть давать ответы (в виде чисел, графиков, таблиц, отчётов) за приемлемое время, с приемлемыми затратами труда и средств (включая затраты на разработку самой модели) и в удобном для пользователя виде. В частности, эффективными должны быть модели реального времени, например, в компьютеризированных системах управления движением, технологическим процессом. Они должны выдавать результаты со скоростью или быстрее реального процесса. Например, процесса в атомном реакторе. Конечно, эффективная модель должна быть адекватной, а ответы – правильными. Не следует забывать, что «любая сложная проблема имеет простое, понятное всем неправильное решение» (научный фольклор), основанное на неадекватной модели. А хорошая модель находится на «узкой полосе между пустыней чрезмерного упрощения и болотом чрезмерного усложнения» (Беллман).

5. Управляемость. Модель должна обеспечивать возможности изменения своих параметров, в обязательном порядке – тех, которые соответствуют управлениям («рулям») моделируемой системы.

Экспертная задача в анализе систем

Математическое моделирование является основным методом изучения сложных систем. В нашей терминологии – методом анализа систем, методом решения экспертной задачи системного анализа.

При моделировании свойства одного объекта переносятся на другой таким образом, чтобы процессы, структуры были изоморфными, аналогичными по форме, не смотря на различную «физическую» сущность. Тогда наблюдая за моделью (например, проводя расчёты на компьютере и анализируя результаты) исследователь может делать выводы о поведении системы, её функциях, интегративных (эмерджентных) свойствах. А также исследовать влияние внутренних и внешних факторов и оптимизировать систему. То есть модели помогают обоснованно решать задачи исследования систем (если модели адекватные, конечно).

Экспертная задача имеет своими целями:

а) понимание и б) прогнозирование.

Решение экспертной задачи должно обеспечить:

а) наблюдаемость системы – адекватное описание её работы и возможность прогнозирования её поведения при различных сценариях;

б) управляемость – определение возможностей воздействия на систему для достижения желаемых целей.

Решение экспертной задачи является основой, базой для решения проектной (конструктивной) задачи системного анализа: проектирования системы, направленной на эффективное достижение поставленных целей.

То есть анализ системы должен предшествовать анализу (и выявлению) проблем с ней связанных. Проект, для которого не решена экспертная задача в теории систем называется утопией [Жилин]. Утопические проекты не всегда являются фантазиями, досужими выдумками. Чаще они преследуют скрытые цели (не декларируемые). Например, получить финансирование или известность.

Вернемся к экспертной задаче. Она – это, по сути, реализация научного метода применительно к анализу систем. Точнее, естественнонаучного, относящегося к естественным наукам, к science.

Схематическое описание этого метода дано австрийским философом Карлом Поппером. Это так называемая «дедуктивно-номологическая» модель. Или «модель D-N». Как и всякая модель, она является упрощенной и идеализированной версией реальности.

Модель D-N построена на утверждениях трех типов:

- конкретные исходные условия;

- конкретные конечные условия;

- универсально верные обобщения («законы»).

Комбинируя некоторый структурированный набор обобщений (т.е. модель системы в нашем случае) с известными более или менее точно исходными условиями, мы получаем прогнозы. Прогноз – это ответ на первый вопрос экспертной задачи: «что будет, если…?». В исследований операций это называется прямой задачей: определить значение критериев качества (целевых функций) при заданных исходных данных.

Комбинируя набор обобщений (модель) с конечными условиями, мы получаем объяснения. Объяснения – это ответ на второй вопрос экспертной задачи: «почему система функционирует именно таким образом?»

Наконец, сопоставление известных исходных данных с известными конечными условиями (состояниями) дает возможность подвергнуть проверке (тестированию, верификации) «универсальные обобщения» (в нашем, более скромном случае – разработанную модель системы).

В D-N существует симметрия между прогнозами и объяснениями: их можно поменять местами. Это основано на обратимости времени в ньютоновской динамике, что говорит, между прочим, об ограниченности D-N модели. «Стрела времени» (необратимость реальных процессов) несколько нарушает симметрию между прогнозом и объяснением, то есть между прямой и обратной задачами [Саати]. Необратимость в природе связана с неустойчивостью и хаосом, этими проблемами занимается наука синергетика.

С проверкой, тестированием дело обстоит иначе: никакой объем тестирования не может доказать, что обобщение «универсально истинно». Зато можно определить границы применимости.

Полная верификация принципиально невозможна, возможна лишь фальсификация, т.е. опровержение универсальности. Именно возможность опровержения отличает научную теорию от спекулятивной (умозрительной, непроверяемой в принципе) теории.

Асимметрия между верификацией и фальсификацией наряду с симметрией между прогнозом и объяснением – таковы две основные характеристики схемы Поппера [Сорос].

Рассмотрим теперь поведение человека и, соответственно, организации, эргативной системы. Подчиняются ли люди, эргативные системы, универсально действующим законам, которые могут быть сформулированы в рамках D-N модели? Конечно, как часть физического мира, они им подчиняются. Но в человеческом (шире - целенаправленном) поведении существуют три аспекта: предвидение (моделирование) будущего, предпочтение и процесс принятия решений. Эти свойства отличают поведение целенаправленных, эргативных систем от поведения объектов и систем, изучаемых естественными науками.

А системный анализ определяется как научная дисциплина, занимающаяся исследования проблем принятия решений в сложных системах в условиях неопределенности и учета многих факторов, относящихся к будущему. То есть в системном анализе симметрия между прогнозом и объяснением нарушается: будущее может влиять на настоящее. Для моделирования и проектирования желаемого будущего предназначается проектная задача, связанная с анализом проблем, которыми занимаются в следующем разделе курса.

Свойства сложных систем

Сложные системы как природные, так и искусственные обладают двумя важными качествами:

1) наличием нескольких дискретных состояний;

2) способностью находиться в данном состоянии в широком диапазоне внешних воздействий (гомеостаз и гомеокинез).

Эргативные системы наряду с этими свойствами, как отмечалось, обладают целенаправленностью (стремлением к прогнозируемому и желаемому будущему). В частности, они обладают способностью целенаправленно реагировать на внешние воздействия.

Математические модели систем должны учитывать эти свойства. В системном анализе широко применяются модели из смежных наук, в первую очередь – из исследования операций, теории управления, синергетики.

Объединение таких «частных» моделей в одной большой модели дает системный эффект «совместного действия» - синергетический эффект.

Это соответствует одному из принципов системного подхода – множественности рассмотрения.

Но наряду с моделями и методами из «смежных» наук в системном анализе существуют собственные методы. В анализе систем – это системная динамика, агентное моделирование, интегральное моделирование; В анализе проблем – это методы многокритериального сравнительного анализа и поддержки принятия решений.

Проблемные ситуации в анализе систем

Проблема (системная задача) - это, как отмечалось ранее, сложная многофакторная неопределенная задача, имеющая несколько допустимых решений (если она их имеет вообще – или не одного, или несколько).

Различают три проблемные ситуации в анализе и моделировании [Хомяков].

1) Хорошо структурированные проблемы. Здесь мы можем построить адекватную количественную модель (лучше - физическую) и исследовать её, опираясь на математические методы.

2) Слабо структурированные проблемы. Мы не можем построить «полностью количественную» модель, но можем построить модель (или иерархию моделей) на основе системного подхода, вербальных и количественных методов системного анализа.

3) Неструктурируемые проблемы. Мы не можем построить количественную модель, применяя методы частных наук и системного анализа, поэтому можем и должны использовать системы и проблемы только при помощи естественного или профессионального языка на основе знаний и опыта.

Собственной сферой системного анализа являются слабо структурированные проблемы.

Но! Применение принципов системного подхода весьма полезно для разработки моделей хорошо структурированных проблем и в анализе результатов моделирования. Современный системный анализ имеет методы для решения неструктурируемых проблем практически без использования математики. Это вербальная аналитика, вербальный анализ решений, так называемые неформальные и эвристические методы. То есть системный анализ ведёт наступление на неформализуемые (пока что) проблемы.

И в этом одно из достоинств системного анализа: он находится между формальными и гуманитарными науками, использует из методы, но имеет и собственный инструментарий для решения системных задач.

Снова перечислим основные системные задачи: исследование, прогнозирование относятся к экспертной задаче; проектирование, управление – к проектной задаче

Иерархия моделей в анализе систем и проблем

Процесс разработки моделей сложной системы имеет такие иерархические уровни, такую последовательность.

1) Структурная модель («анатомия системы») – подсистемы, элементы и связи.

2) Функциональная модель («физиология системы») – на качественном уровне описывает функции, интегративные свойства системы и влияние на них внешних воздействий.

3) Динамическая модель («поведение системы») – описывает изменение состояний системы во времени и пространстве, описывает по возможности количественно.

4) Имитационная модель – описывает поведение системы в различных, в том числе и случайных условиях (случайных внешних воздействиях или случайных изменениях параметров и структуры системы).

5) Оптимизационная модель – служит для поиска лучших проектных параметров.

Иерархия моделей по сложности

Модель редко создаётся «сразу». Сначала создаётся некоторая упрощённая модель, которая затем уточняется и усложняется.

Введём очень важные понятия:

Базовая модель – это наиболее простая модель системы, содержащая характерные, существенные особенности. Дальше упрощать нельзя. Базовые модели имеются во всех точных науках. Например, базовой моделью теории колебаний является математический маятник, совершающий малые колебания (гармонический осциллятор), базовой моделью ракетодинамики является «точка переменной массы», базовой моделью механики – абсолютно твёрдое тело, базовой моделью термодинамики – идеальный газ, гидродинамики – идеальная жидкость.

Базовые модели важны в трёх отношениях.

Во-первых, они являются основой теорий, обеспечивающей понимание, допускают аналитические решения («формулы») и качественный анализ.

Во-вторых, они являются фундаментом (или блоками) для построения моделей больших и сложных систем вплоть до имитационных моделей. По мере усложнения модель сложной системы становится трудной для понимания, недоступной для аналитического анализа и только сочетание компьютерного эксперимента (о нём ниже) и теоретического анализа на основе базовых моделей позволяет объяснить и понять поведение сложной системы.

В-третьих, базовых моделей немного, не смотря на разнообразие систем и процессов реального мира. Поэтому каждая из них, как правило, описывает широкий класс явлений. Так модель гармонического осциллятора служит основой и в описании колебаний конструкций, и в теории звука, и в теории электрических цепей. Простые математические модели оказываются весьма содержательными и универсальными. На их основе можно представить качественные особенности поведения сложных систем, даже предсказывать неизвестные ранее явления.

И, наконец, базовые модели в предметной области являются основными на начальных этапах проектирования систем. Так для проектирования архитектуры спутниковых систем используется простая модель движения «малого» тела в центральном поле тяготения планеты (one-body problem).

Универсальность и глубина базовых математических моделей служат основой для создания междисциплинарных подходов в изучении сложных систем и процессов (в таких науках, как кибернетика, синергетика да и системный анализ).

Создание сложных моделей в «частных науках» происходит, как правило, на основе последовательного уточнения, учёта всё большего числа факторов, уточнения базовых объектов. Так, абсолютно упругое тело статики заменяется в сопротивлении материалов упругим телом, подчиняющимся линейному закону Гука. Идеальная жидкость в гидродинамике заменяется вязкой жидкостью, в газовой динамике – сжимаемым газом. В расчётах орбит спутников учитываются всё более тонкие эффекты, такие, как несферичность поля тяготения Земли, разреженная атмосфера, влияние поля тяготения Луны, солнечный ветер, релятивистские поправки…

В системном проектировании (системотехнике) модели сложных систем разрабатываются на основе принципов системного подхода с использованием двух основных операций – декомпозиции и агрегирования. Существует два основных вида декомпозиции – по процессам (функциональная декомпозиция, так называемый структурный подход) и по объектам (объектно-ориентированный подход).

Современный этап развития техники математического моделирования характеризуется тем, что разработаны и развиваются программные пакеты для структурного, функционального, динамического, имитационного моделирования. Как примеры можно назвать GPSS, Simulink, AnyLogic, Allfusion (BPWin). Эти пакеты позволяют создавать структурные, функциональные и даже имитационные модели технических и организационных систем, выполнять компьютерные эксперименты, оптимизировать системы различного назначения. Использование программных средств резко повышает производительность труда разработчиков модели. Но надо помнить, что разработку моделей принципиально новых систем (хотя такое случается редко) надо вести с теоретических основ, с базовых моделей.

Методы изучения сложных систем

По крупному» их можно разделить на три большие группы: качественные, количественные и смешанные.

1) Качественные методы – их основой служит объём знаний в данной предметной области, а основным инструментом – естественный и профессиональный язык, логика. До примерно 20-х – 30-х годов 20-го века большинство «классических описательных наук» (биология, медицина, экономика) использовали в основном качественные методы и продолжают их использовать. И во всех других науках и сферах человеческой деятельности эти методы используются, занимая более или менее значительное место. И достоинства и недостатки этих методов очевидны.

Качественные методы можно разделить на вербальную аналитику (логичное, рациональное объяснение и прогнозирование средствами языка, схемами) и эвристические («неформальные»).

К эвристическим методам относятся такие методы, как:

1) морфологический анализ;

2) метод аналогий;

3) экспертные оценки (например, метод Делфи);

4) «творческие» (изобретательские методы): мозговой штурм, синоптика, теория решения изобретательских задач…

Отметим, что для ряда эвристических и изобретательных методов разработаны формализованные модели и даже программные продукты («машина изобретений», например). То есть и по этому направлению идёт наступление, перевод ранее неструктурируемых проблем в слабо структурируемые проблемы.

2) Количественные (формализованные) методы – это как раз построение математических моделей и их анализ, проведение компьютерных экспериментов, сфера математического моделирования и исследования операций, математического программирования.

3) Смешанные методы – это сфера системного анализа. Используются количественные методы, экспертные оценки, методы анализа решений, эвристические методы. Мы их рассмотрим позже – в анализе проблем, где они собственно и используются.

Количественные модели – это собственно и есть моделирование математическое. Для сложных систем, изучаемых в системном анализе – это практически всегда компьютерное моделирование. Но не следует забывать о базовых моделях и аналитических решениях, которые могут служить исходными оценками и «ориентирами» при построении сложных моделей и анализе результатов.

Простые модели очень важны на начальном этапе проектирования технической системы – при оценке реализуемости системы. Здесь выработан важный практический принцип – «презумпция реализуемости»: при разработке простой, базовой модели системы все допущения принимаются «в плюс», в пользу данной системы. Если при этих допущения модель покажет, что проектируемая система не сможет выполнить заявленные задачи (например, ракета-носитель не сможет выводить на орбиту спутники и космические корабли), то следует прекратить дальнейшую разработку системы (её моделей) до уточнения задач. Или совсем прекратить.

Некоторые классы математических моделей сложных систем

Перейдём к описанию основных классов математических моделей с точки зрения применяемого в них математического аппарата. Ещё раз отметим, что модели (особенно имитационные) реальных сложных систем как правило, являются гибридными, т. е. в них используется (в разных блоках) разный математический аппарат.

Начнём с динамических моделей, наиболее часто применяемых в частных науках (экономика, экология, демография…). Эти модели применяются и в системном анализе. Они включают в себя следующие виды (классы). Они принадлежат к так называемым физичным (другое название, довольно корявое – физикалистские модели) моделям – моделям «прозрачного ящика».

1. Матричные модели

Это алгебраические или дифференциальные линейные модели, они имеют вид:

· алгебраические (дискретные) модели:

(4.1)

· дифференциальные (непрерывные) модели:

(4.2)

Здесь вектор (набор) переменных параметров состояния системы, матрица коэффициентов (квадратная). Матрица в общем случае может быть переменной: её элементы (все или некоторые) – известные функции времени: . Размерность вектора и размерность матрицы должны быть согласованы. Соответственно: и .

Напомним, что производная по времени – это скорость изменения переменной состояния.

Смысл матричной модели прост и вполне понятен: новое состояние любого параметра состояния системы определяется состоянием всех таких параметров в предшествующий момент времени. В дискретных моделях время изменяется с некоторым конечным шагом, в непрерывных моделях – это непрерывное физическое время.

Теория линейных систем хорошо разработана, поэтому матричные модели позволяют проводить аналитические исследования процессов, а не только компьютерные эксперименты. Такие модели используются в экономике (межотраслевые балансы), в экологии (динамика популяций), в теории управления.

Из (4.1) и (4.2) видно, что матричные модели применяются только тогда, когда вектор состояний системы в последующий момент времени (непрерывного или дискретного времени) можно представить в виде линейной комбинации параметров состояния системы в предыдущий момент времени.

Но (увы, или, скорее, к счастью) системы и процессы в реальном макроскопическом мире, как правило, нелинейны. Поэтому матричные модели в виде (4.1) и (4.2) применимы далеко не всегда. Очевидный недостаток этих моделей – невозможность с их помощью описать качественные смены состояния сложных систем, их развитие, усложнение, разрушение. Этим занимается так называемая «нелинейная наука» - синергетика.

2. Динамические балансовые модели

Наряду с линейными (как правило, матричными) и нелинейными динамическими моделями имеется ещё один важный класс динамических моделей – балансовые модели. Они используют тот же математический аппарат – обыкновенные дифференциальные уравнения и алгебраические уравнения, но отличаются подходы к моделированию, «взглядом» на моделируемую систему. Система в них представляется как совокупность потоков вещества и энергии. Балансы – это сохранение «входящих» и «исходящих» потоков с учётом их преобразований внутри системы. Такие балансы рассчитываются на каждом этапе моделирования. В балансы могут входить информационные составляющие, например, финансовые ресурсы. Но с учётом их специфики и принципов обмена.

Видно, что балансовые модели могут применяться для моделирования широкого диапазона проблем в экономике, экологии, функционировании технических систем, предприятий, бизнес-процессов. Короче говоря, для моделирования процессов в разнообразных, в том числе – комплексных технических и производственных системах.

Это – основной класс моделей для таких целей. Имеется большая литература по ним и довольно много программных средств, позволяющих строить такие модели.

Важным частным случаем динамических балансовых моделей являются «резервуарные» (компартментальные – ну и слово!) модели. Они построены на «гидродинамической аналогии»: моделируемая система представляется в виде системы различных резервуаров («компартментов»), находящихся на разных уровнях и связанных между собой копалами обмена массами, энергией различных видов, деньгами и т. п.

3. Системно-динамические модели

Они являются развитием динамических балансовых моделей. В этих моделях сложные системы (очень сложные и большие) исследуются на высоком уровне абстракции. Исследователи абстрагируются от индивидуальных объектов системы и рассматривают только агрегированные количественные характеристики потоков этих объектов.

В системно-динамических моделях (по сравнению с резервуарными моделями) важную роль играют обратные связи, перестройки структуры системы (логика процессов). В математическом аппарате наряду с обычными дифференциальными уравнениями используются дифференциальные уравнения с запаздывающим аргументом:

где запаздывающий аргумент, .

То есть поведение системы зависит не только от текущего состояния, но и от прошлого, отстающего на некоторый конечный интервал времени (эти интервалы для разных переменных могут быть разными).

В настоящее время метод системной динамики рассматривается как один из главных методов системного анализа, а именно – анализа систем. Системная динамика – это эффективный подход к анализу таких проблем, как производственный процесс, анализ рынка, управление поставками и сбыта, логистика.

Применение методологии системной динамики даёт системному аналитику понимание эффектов от внешних воздействий и изменений внутренней структуры и параметров системы. Это позволяет сравнивать альтернативные решения и выбирать оптимальные варианты, что, собственно, и является основной задачей анализа проблем, как мы увидим в следующей части курса.

Только изучение динамики всей системы со всеми её связями и временными задержками может привести к корректному пониманию процессов всей системы. Это и составляет основную идею системного мышления [Карпов]. Системную динамику часто непосредственно связывают с системным мышлением, и это правильно. Но системное мышление имеет и другие аспекты, связанные с принятием решений.

4. Интегральное моделирование

Его можно рассматривать как одно из направлений системной динамики. Основная идея: максимально ограничить количество переменных состояния системы, но при этом максимально увеличить количество учитываемых связей между ними [Хомяков]. Основная цель интегрального моделирования: исследование (имитация) динамики изменения структуры системы (процессов самоорганизации и дезорганизации системы, моментов «фазовых» переходов из одного состояния в другое). Это в некотором смысле роднит интегральное моделирование с синергетикой. Можно сказать, что интегральное моделирование – это компьютерная синергетика. Интегральное моделирование показала свою эффективность в такой важной сфере, как прогнозирование кризисов и катастроф [Хомяков].

Все рассмотренные выше типы моделей принадлежат к так называемым физичным (другое название, довольно корявое – физикалистским) моделям – моделям «прозрачного ящика».

К моделям «чёрного ящика» относятся в первую очередь следующие модели.

5. Статистические модели

В этих моделях используется математический аппарат статистики, случайного эксперимента (метод Монте-Карло), а также регрессионный анализ, марковские цепи, «интеллектуальный анализ данных» (data mining).

При построении статистических моделей исследователь стремится устранить связь между входными и выходными параметрами системы, «не вникая» в её структуру и внутренние процессы.

Так, линейная регрессионная модель имеет вид:

(4.6)

Здесь выходная характеристика, вектор входных характеристик («факторов»), постоянные коэффициенты, 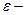случайная величина с нулевым математическим ожиданием и заданной дисперсией. С математической точки зрения с помощью модели (4.6) ищется система коэффициентов , задающая гиперплоскость в мерном пространстве некоторым наилучшим образом, например по методу наименьших квадратов или методу наименьших модулей.

Видны основные недостатки такой модели.

1. Необходим большой объём надёжных экспериментальных данных.

2. Реальный вид зависимости практически всегда отличается от заданного в модели линейного вида.

3. Модель (как и всякая линейная модель) не способна предсказывать качественные изменения в состоянии системы.

4. Для статистических моделей не ясны границы их применимости, где они перестают работать.

6. Модели стохастической динамики

Они объединяют динамический и вероятностный подходы.

Такая модель имеет вид:

(4.7)

где вектор переменных состояния (характеристик системы); вектор внешних воздействий (управлений); случайный вектор.

Если исключить случайный вектор , то модель (4.7) становится моделью динамической системы, например, балансовой; влияние случайных воздействий (их можно разделить на влияние воздействия и случайные изменения внутренних коэффициентов) делают эту модель стохастической, привносит вероятностный характер.

Стохастические модели используются в моделировании динамики энергетических и транспортных систем (поездов, например) работы систем энергоснабжения, в системной динамике.

Дата добавления: 2015-10-23