Пример решения К.Р. для заочников по математике по теме

«Линейная алгебра и аналитическая геометрия», 1 семестр

Задача 1. Дана матрица Найти

Решение.

Через определитель и алгебраические дополнения найдем обратную матрицу:

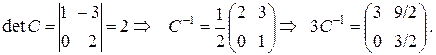
Задача 2. Решить систему уравнений

a) методом Крамера, b) матричным методом, c) методом Гаусса.

Решение. a) метод Крамера. Считаем определители разложением по первой строке (столбцы по очереди меняются на столбец свободных членов)

Теперь найдем ответ по формулам

b) матричный метод. Найдем обратную матрицу по формуле

где - алгебраическое дополнение элемента

Теперь ответ найдем по формуле

c) метод Гаусса. Делаем элементарные преобразования расширенной матрицы, нумеруем строки римскими цифрами.

. Получили диагональную матрицу, начинаем решать с последнего уравнения (обратный ход):

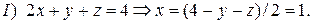
Отметим, что во всех трех способах ответы совпали.

Задача 3. В каноническом базисе даны координаты векторов

a) Показать, что - базис в R³.

b) Записать матрицу перехода от базиса к базису и разложить вектор в этом базисе.

Решение. a) Составим определитель из координат векторов :

Определитель из координат не равен нулю, значит, эти векторы составляют базис в R³.

b) Матрица перехода от базиса к базису имеет вид (координаты векторов записаны по столбцам)

.

Координаты вектора в базисе найдем из уравнения

или в матричной форме

Решим эту систему методом Крамера (см. задачу 2).

Задача 4. Дана матрица

1) Для системы , где X – 5-мерный вектор-столбец неизвестных

найти

a) фундаментальную систему решений,

b) общее решение,

c) частное решение.

2) Пусть C – расширенная матрица системы 4-х уравнений с 4-мя неизвестными. Решить эту систему, исследовав совместность по теореме Кронекера-Капелли.

Решение. 1) Решим систему методом Гаусса, совершая элементарные преобразования строк, нумеруя строки римскими цифрами, обнуляем элементы ниже диагонали.

Пусть x ₅ – свободное неизвестное. Последнее уравнение имеет вид

из третьего уравнения найдем

из второго уравнения найдем

из первого уравнения найдем

a) Общее решение имеет вид (x ₅ – свободное неизвестное):

b) Частное решение найдем, положив x ₅=1:

c) Отсюда фундаментальное решение запишем в виде

. Здесь t – любое число.

2) Ранг основной матрицы равен 4 и совпадает с рангом расширенной матрицы, поэтому система совместна по теореме Кронекера-Капелли.

Расширенная матрица уже приведена к виду (см. выше)

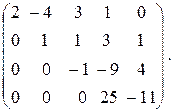
Совершая обратный ход (начиная с последнего уравнения), последовательно найдем: из четвертого уравнения

из третьего уравнения

из второго уравнения

из первого уравнения

Задача 5. Даны четыре точки – вершины пирамиды с координатами

Найти:

а)

б) угол между ребрами

в) площадь грани

г) объем пирамиды;

д) уравнения прямых

е) уравнения плоскостей

ж) угол между плоскостями

з) высоту пирамиды как расстояние от точки A ₄ до плоскости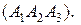

Решение.

а)

б)

в) Искомая площадь S равна половине модуля векторного произведения векторов:

,

г) Искомый объем V равен одной шестой модуля смешанного произведения векторов:

,

д) Каноническое уравнение прямой

Каноническое уравнение прямой

е) Уравнение плоскости найдем как смешанное произведение векторов (M (x, y, z) – текущая точка плоскости)

Уравнение плоскости найдем как смешанное произведение векторов (M (x, y, z) – текущая точка плоскости)

ж) Угол между плоскостями равен углу между нормалями к этим плоскостям. Из пункта е) видно, что для плоскости нормаль

а для плоскости нормаль значит, косинус угла y между этими плоскостями равен

з) Высота пирамиды h вычисляется через ее объем V (см. пункт г)) и площадь основания S (см. пункт в)) по формуле

Дата добавления: 2015-10-24