
|
Читайте также: |
Незатухающие гармонические колебания
Гармонические колебания совершаются под действием упругих или квазиупругих (подобные упругим) сил, описываемых законом Гука:
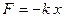 ,
,
где F – сила упругости;
х –смещение;
k – коэффициент упругости или жесткости.
Согласно ІІ закону Ньютона 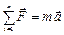 , где а – ускорение, а =
, где а – ускорение, а =  .
.

| (1) |
Разделим уравнение (1) на массу m и введем обозначение 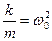 , получим уравнение в виде:
, получим уравнение в виде:
 (2).
(2).
Уравнение (2) – дифференциальное уравнение незатухающих гармонических колебаний.
Его решение имеет вид:  или
или 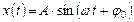 .
.
Характеристики незатухающих гармонических колебаний:
х – смещение; А – амплитуда; Т – период;  – частота;
– частота;  – циклическая частота,
– циклическая частота, 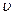 – скорость;
– скорость; 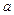 – ускорение,
– ускорение, 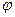 – фаза;
– фаза; 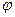 0 – начальная фаза, Е – полная энергия.
0 – начальная фаза, Е – полная энергия.
Формулы:
 – число колебаний, – число колебаний, 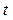 – время, за которое совершается N колебаний; – время, за которое совершается N колебаний;
|
 , ,  ; ; 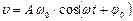 или или  ; ;
|
 или или  ; ;
|
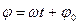 – фаза незатухающих гармонических колебаний; – фаза незатухающих гармонических колебаний;
|
 – полная энергия гармонических колебаний. – полная энергия гармонических колебаний.
|
Затухающие гармонические колебания
В реальных системах, участвующих в колебательном движении, всегда присутствуют силы трения (сопротивления):
 ,
, 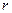 – коэффициент сопротивления;
– коэффициент сопротивления;  – скорость.
– скорость.
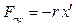 .
.
Тогда ІІ закон Ньютона запишем:



| (2) |
Введем обозначения 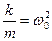 ,
, 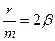 , где
, где  – коэффициент затухания.
– коэффициент затухания.
Уравнение (2) запишем в виде:
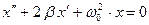
| (3) |
Уравнение (3) – дифференциальное уравнение затухающих колебаний.
Его решение 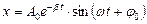 , где
, где
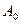 – амплитуда колебаний в начальный момент времени;
– амплитуда колебаний в начальный момент времени;
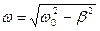 – циклическая частота затухающих колебаний.
– циклическая частота затухающих колебаний.
Амплитуда колебаний изменяется по экспоненциальному закону:
 .
.
Характеристики:
1) 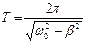 – период затухающих колебаний; 2)
– период затухающих колебаний; 2) 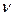 – частота затухающих колебаний;
– частота затухающих колебаний;  – собственная частота колебательной системы;
– собственная частота колебательной системы;
3) логарифмический декремент затухания (характеризует скорость убывания амплитуды): 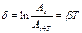 .
.
Вынужденные колебания
Для получения незатухающих колебаний необходимо воздействие внешней силы, работа которой восполняла бы вызванное силами сопротивлений уменьшение энергии колеблющейся системы. Такие колебания называются вынужденными.
Закон изменения внешней силы:  , где
, где  – амплитуда внешней силы.
– амплитуда внешней силы.
ІІ закон Ньютона запишем в виде

Введем обозначения  .
.
Уравнение вынужденных колебаний имеет вид:
 .
.
Решение этого уравнения в установившемся режиме:
 ,
,
где 
| (4) |

 – частота вынужденных колебаний.
– частота вынужденных колебаний.
Из формулы (4), когда  , амплитуда достигает максимального значения. Это явление называется резонансом.
, амплитуда достигает максимального значения. Это явление называется резонансом.
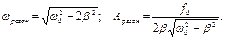
5.Волна – это процесс распространения колебаний в упругой среде.
Уравнение волны выражает зависимость смещения колеблющейся точки, участвующей в волновом процессе, от координаты ее равновесного положения и времени: S = f (x;t).
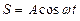

|
Если S и X направлены вдоль одной прямой, то волна продольная, если они взаимно перпендикулярны, то волна поперечная.
Уравнение в точке "0" имеет вид  . Фронт волны дойдет до точки "х" с запаздыванием за время
. Фронт волны дойдет до точки "х" с запаздыванием за время  .
.
Уравнение волны имеет вид  .
.
Характеристики волны:
S – смещение, А – амплитуда,  – частота, Т – период,
– частота, Т – период,  – циклическая частота,
– циклическая частота,  – скорость.
– скорость.
 – фаза волны,
– фаза волны, 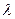 – длина волны.
– длина волны.
Длиной волны называется расстояние между двумя точками, фазы которых в один и тот же момент времени отличаются на  .
.

Фронт волны – совокупность точек имеющих одновременно одинаковую фазу.
Поток энергии равен отношению энергии, переносимой волнами через некоторую поверхность, к времени, в течении которого эта энергия перенесена:
 ,
, 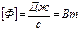 .
.
Интенсивность:  ,
, 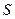 –площадь,
–площадь, 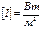 .
.
Вектор интенсивности, показывающий направление распространения волн и равный потоку энергии волн через единичную площадь, перпендикулярную этому направлению, называется вектором Умова.
 – плотность вещества.
– плотность вещества.
7.Звук – это механическая волна, частота которой лежит в пределах  ,
,  – инфразвук,
– инфразвук, 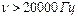 – ультразвук.
– ультразвук.
Различают музыкальные тоны (это монохроматическая волна с одной частотой или состоящая из простых волн с дискретным набором частот – сложный тон).
Шум – это механическая волна с непрерывным спектром и хаотически изменяющимися амплитудами и частотами.
Характеристики звука
Энергетической характеристикой звука является интенсивность.
На практике для оценки звука удобнее использовать звуковое давление.
Звуковое давление (  ) – это избыток давления в звуковой волне над атмосферным.
) – это избыток давления в звуковой волне над атмосферным.
 ,
,  ,
,
где 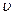 – скорость звука,
– скорость звука, 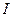 – интенсивность звуковой волны.
– интенсивность звуковой волны.
Характеристики слухового ощущения
Высота тона – зависит от частоты, чем выше частота, тем выше звук (определяется минимальной частотой акустического спектра, рис. 14).
Тембр – "окраска" звука, зависит от состава акустического спектра (совокупность простых волн, образующих сложные).
Громкость – субъективная характеристика звука, которая характеризует уровень слухового ощущения.
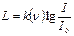
 – коэффициент пропорциональности, зависящий от частоты и интенсивности;
– коэффициент пропорциональности, зависящий от частоты и интенсивности;
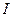 – интенсивность исследуемого звука;
– интенсивность исследуемого звука;
 – порог слышимости;
– порог слышимости; 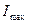 – порог болевых ощущений.
– порог болевых ощущений.
Для  ,
, 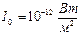 ,
,  .
.
Единицей измерения громкости, является Белл – это громкость звука, которая при  имеет
имеет 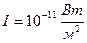 , при этом
, при этом  .
.
 . 1 Децибел (дБ) или 1 фон = 0,1 Б.
. 1 Децибел (дБ) или 1 фон = 0,1 Б.
Зависимость громкости от частоты учитывают с помощью кривых равных громкостей, получаемых экспериментально, и используется для оценки дефектов слуха. Метод измерения остроты слуха называется аудиометрия. Прибор для измерения громкости называется шумомер. Норма громкости звука должна составлять 40 – 60 дБ.
8. Ультразвук – это механическая волна с частотой  . Верхним пределом ультразвуковой частоты можно считать 10 9 – 10 10 Гц.
. Верхним пределом ультразвуковой частоты можно считать 10 9 – 10 10 Гц.
В 1880 г. П. Кюри открыл пьезоэффект.
Для получения ультразвука используют ультразвуковые излучатели, основанные на обратном пьезоэлектрическом эффекте: к электродам прикладывается переменное электрическое поле и пластинка кварца (сегнетовой соли, титаната бария) начинает вибрировать, излучая механическую волну определенной частоты.
Приемник ультразвука использует прямой пьезоэффект: возникновение разности потенциалов на гранях пьезокристалла при его деформации.
Дата добавления: 2015-10-23; просмотров: 124 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ИССЛЕДОВАНИЕ БИОСОВМЕСТИМОСТИ ФРАГМЕНТОВ ИСКУССТВЕННЫХ МЕХАНИЧЕСКИХ КЛАПАНОВ СЕРДЦА С НАНЕСЕННЫМИ ПОКРЫТИЯМИ НА ОСНОВЕ МОДИФИЦИРОВАННОГО УГЛЕРОДА | | | Свойства ультразвука используемые в медицине |