Сетевой метод

Чтобы рассчитать сетевым методом основные параметры алгоритма, необходимо на укрупненной ГСА выделить циклы. Для исходного алгоритма, взятого в примере, выделяются три цикла (рис. 1.8).

Сначала рассчитывают вложенные циклы, поэтому рассмотрим первый цикл - цикл С1 (см. рис. 1.9).

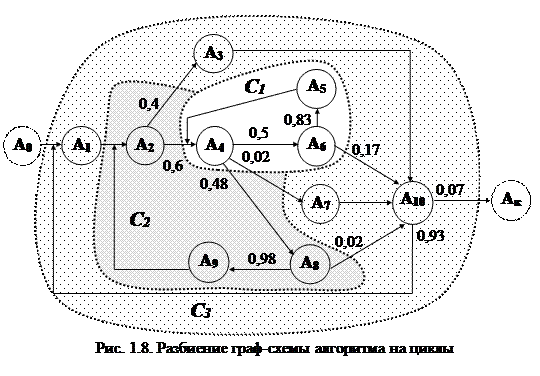Определим вероятность выхода из цикла Р_вых и вероятность зацикливания Р_ц. Вероятность выхода из цикла будет равна сумме всех выходов (т.к. выход не единственный).

Р_вых=0,48+0,02+0,5´0,17=0,585 Þ Р_ц=1 - Р_вых=0,415.

Таким образом, среднее число повторений цикла С1 равняется

n_C1=1/P_вых=1,71.

Найдем трудоемкость тела цикла: q^t_C1=ån_iq^V_i, где значение q^V_i - это трудоемкость вершины V_ai, соответствующей оператору счета, входящей в i-ю операторную вершину укрупненной ГСА.

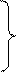n₄=1 q^V₄=50

n₆=0,5 q^V₆=60 => q^t_C1=50+30+12,45=92,45 операций

n₅=0,83* n₆=0,415 q^V₅=30

Таким образом средняя трудоемкость цикла С1 равна

q_C1= q^t_C1´n_C1=158,09 операций.

Для определения минимальной и максимальной трудоемкости цикла С1 необходимо определить минимальный и максимальный пути прохождения по циклу.

Максимальная qmax_С1 и минимальная qmin_С1 трудоемкость цикла определяется как сумма трудоемкостей всех вершин, составляющих соответственно максимальный и минимальный пути цикла, умноженной на среднее число повторений цикла n_C1

qmin_С1=50´1,71=85,5 операций;

qmax_С1=(50+60+30+50+60) ´1,71=427,5 операций.

Цикл С2. После расчета вложенных циклов они представляются на графе других циклов в виде вершины, в данном случае цикл С1 представляется вершиной С1 (рис. 1.10).

В цикле С2 кроме вероятности выхода из цикла необходимо определить вероятности выхода из цикла С1. Так как сумма вероятностей выходов из С1 равна 1, то, например, р_{C1 8}=0,48/(0,17+0,02+0,48)=0,72. Аналогично определяются и остальные вероятности.

Р_вых=0,4+0,6´(0,25+0,03)+0,6´0,72´0,02=0,577;

Р_ц=0,423;

Среднее число повторений цикла С2 равняется

n_C2=1/P_вых=1,73.

Трудоемкость тела цикла определяется как

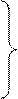
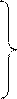n₂=1 q^V₂=0

n_C1=0,6 q^V_C1=158,09 => q^t_C2=181,254 операций,

n₈=0,72´ n_C1=0,432 q^V₈=200

n₉=0,98´ n₈=0,423 q^V₉=0

а средняя трудоемкость цикла С2 равна

q_C2= q^t_C2´ n_C2=313,57 операций.

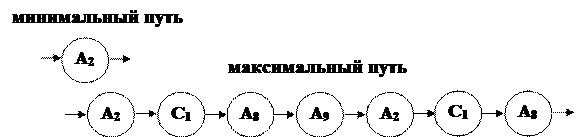Минимальный путь для цикла С2 будет состоять из одной вершины.

Так как в вершине А2 отсутствует оператор счета, то минимальная трудоемкость цикла С2 равно нулю qmin_С2=0 операций.

Максимальный путь равен полному прохождению цикла, и максимальная трудоемкость цикла С2 равна

qmax_С2=(0+427,5+200+0+0+427,5+200) ´1,73=2171,15 операций.

Цикл С3. Для цикла С3 (рис. 1.11), как и для цикла С2, нужно рассчитать вероятности выхода из цикла С2. Рассуждения аналогичные, но вероятности берутся те, которые уже рассчитывали для С2.

Например: р_{C2 10}=(0,02+0,25)/(0,4+0,03+0,25+0,02)=0,39

Р_вых=0,07;

Р_ц=0,93;

n_C3=14,29.

Трудоемкость тела цикла равна

n₁=1 q^V₁=10

n_C2=1 q^V_C2=313,57

n₃=0,57´ n_C2=0,57 q^V₃=100 => q^t_C3=417,17 операций;

n₇=0,04´ n_C2=0,04 q^V₇=40

n₁₀= n₃+n₇+0,39´ n_C2=1 q^V₁₀=35

а средняя трудоемкость цикла С3 и всего алгоритма определяется как

q_C3= q_ср= q^t_C3´ n_C3= 5961,36 операций.

Для цикла С3 характерно ветвление алгоритма - в вершину А₁₀ идут три дуги. Чтобы рассчитать минимальную и максимальную трудоемкости этого цикла, необходимо вычислить минимальные и максимальные пути соответственно.

Расчет минимальной трудоемкости.

qmin₀=0

qmin₁=10

qmin_С2=0+10=10

qmin₃=100+10=110

qmin₇=40+10=50

qmin₁₀=35+min(qmin₃,qmin_C2,qmin₇)=45

qmin_k=q_min=45´14,29=643,05 операций.

Расчет максимальной трудоемкости.

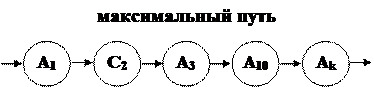qmax₀=0

qmax₁=10

qmax_С2=2171,15+10=2181,15

qmax₃=100+2181,15=2281,15

qmax₇=40+2181,15=2221,15

qmax₁₀=35+max(qmax₃,qmax_C2,qmax₇)=35+2281,15=2316,15

qmax_к=q_max=2316,15´14,29=33097,78 операций.

Таким образом, полученные значения трудоемкостей для цикла С3 и определяют минимальную, среднюю и максимальную трудоемкости всего алгоритма, рассчитанные сетевым методом:

q_min =643,05 операций;

q_ср =5961,36 операций;

q_max =33097,78 операций.

Дата добавления: 2015-10-31