Завдання 4 Розрахунок глобальних пріоритетів альтернатив

Мета – освоєння методів отримання оптимального рішення за багатьма критеріями.

З метою оновлення комп'ютерного парку корпорації необхідно вибрати один із чотирьох типів комп'ютерів, ураховуючи технічний, вартісний, ергономічний аспекти, а також супровід.

Критеріями технічного аспекту є швидкодія, споживання електроенергії, можливості апгрейту (часткового поновлення). На вартісний аспект впливають початкова вартість та вартість щорічного утримання. Ергономічний аспект конкретизується до шумових характеристик, характеристик монітора, зручності роботи з периферійними пристроями.

Оновлення комп’ютерного парку корпорації

Технічний аспект

Вартісний аспект

Ергономічний аспект

Супровід

Комп’ютер типу А

Комп’ютер типу В

Комп’ютер типу С

Комп’ютер типу D

Супровід оцінюється характеристиками гарантії, наявністю гарантійних сервісів у різних областях та можливістю модернізації, оновлення компонентів системи. Відповідну ієрархію зображено на рис. 6.

Рисунок 6 ‑ Ієрархія критеріїв

У результаті опитування експерта отримані наступні матриці попарних порівнянь:

,

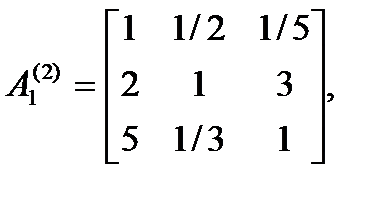
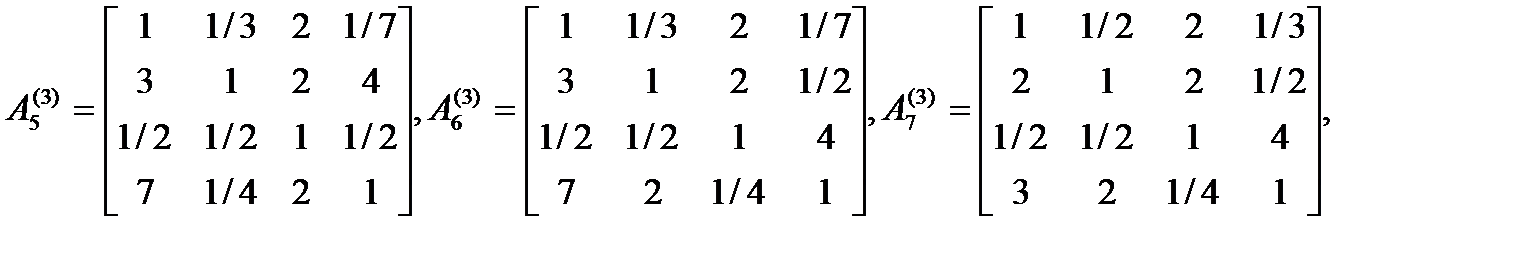
На основі експертних даних побудуйте матриці прямих порівнянь, розрахуйте локальні характеристики вершин ієрархії, виберіть найкращий варіант та оцініть послідовність експерта відносно ієрархії загалом.

Методичні рекомендації щодо виконання завдання

Особливість цього завдання, характерне для практичних завдань управління та оптимізації, полягає в тому, що його рішення не можна задати у формульному вигляді, оскільки початкова інформація представлена у вигляді кількісних та якісних експертних оцінок.

Використовуємо для знаходження найкращого розв’язку метод аналізу ієрархій, оснований на адитивному згортанні, що дозволяє не тільки знайти найкраще рішення, але й оцінити його достовірність. Метод пов'язаний з тим, що рішення приймаються на декількох рівнях: спочатку на рівні критеріїв, потім на рівні альтернатив. Перевагою методу є також його застосованість у нечітких ситуаціях. Завдання формулюється в наступному вигляді.

Нехай є безліч альтернатив (варіантів рішень): В₁, В₂,... В_n. Кожна з альтернатив оцінюється списком критеріїв: K₁, К₂,... К_n.

Зазвичай n < 10; якщо n > 10, то використовуються узагальнені критерії, так щоб їх загальна кількість не перевищувала 10, потім вони піддаються декомпозиції. Потрібно визначити найкраще рішення.

Етапи вирішення задачі:

1. Проводиться попереднє ранжування критеріїв, і вони розташовуються в порядку убування важливості:

В(К₁) > В(К₂) >... > В(К_n).

2. Проводиться попарне порівняння критеріїв за важливістю, згруповані за дев'ятибальною шкалою, і складається відповідна матриця розміру (n х n):

3.Визначається нормалізований вектор пріоритетів (НВП):

а) розраховується середнє геометричне в кожному рядку матриці:

б) розраховується сума середніх геометричних:

Σ = a_i + a₂ +... +а_n;

в) обчислюються компоненти НВП:

Кожен компонент НВП являє собою оцінку важливості відповідного критерію (1-й ‑ першого, 2-й ‑ другого тощо). Слід звернути увагу на те, що оцінки важливості критеріїв у таблиці повинні відповідати попередньо проведеного ранжування (див. п.1).

4. Перевіряється узгодженість оцінок у матриці. Для цього підраховують три характеристики:

а) власне значення матриці:

λ_max = сума елементів 1-го стовпця х 1-й компонент НВП +

+ сума елементів 2-го стовпця х 2-й компонент НВП +

+... + сума елементів n -го стовпця х n -й компонент НВП;

б) індекс узгодження:

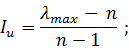
в) відношення узгодженості:

Показник випадкової узгодженості визначають теоретично для випадку, коли оцінки в матриці подані випадковим чином, а сам показник залежить тільки від розміру матриці (табл. 1).

Таблиця 1 ‑ Значення індексу узгодженості для випадкових матриць

Розмір матриці
Випадкова узгодженість			0,58	0,90	1,12	1,24	1,32	1,41	1,45	1,49	1,51	1,48	1,56	1,57	1,59

Оцінки в матриці вважають узгодженими, якщо , в іншому випадку їх треба переглядати.

5. Проводиться попарне порівняння варіантів за кожним критерієм аналогічно тому, як це робилося для критеріїв, і заповнюються відповідні таблиці (табл. 2, табл. 3). Підраховують λ_{max і}, , для кожної таблиці.

Таблиця 2 ‑ Форма таблиці порівняння критеріїв

	K1	К2	...	Кn	НВП
K1
К2
...
Кn
λ max =

Таблиця 3 ‑ Форма таблиці порівняння варіантів за критеріями

K1	В1	В 2	...	В n	НВП
В 1
В 2
...
В n
λmax j =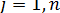

6. Визначають загальний критерій (пріоритет) для кожного варіанта:

К(В_і) = оцінка В₁ за першим критерієм х 1-й компонент НВП +

+ оцінка В₁ за другим критерієм х 2-й компонент НВП +

+... + оцінка В₁ за n-м критерієм * n-й компонент НВП.

Аналогічно підраховують К (В₂), К (В₃) і т.д., при цьому у виразі замінють В_і на В₂, В₃ і т. д. відповідно.

7. Визначають найкраще рішення, для якого значення К є максимальним.

8. Перевіряють вірогідність рішення:

а) підраховують узагальнений індекс узгодження:

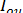= х 1-й компонент НВП + х 2-й компонент НВП +

+... + х n-й компонент НВП;

б) підраховують узагальнене відношення узгодженості:

де 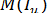для матриць порівняння варіантів за критеріями.

Рішення вважають вірогідним, якщо 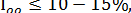у протилежному випадку необхідно коригувати матриці порівняння варіантів за критеріями.

Слід мати на увазі, що для прийняття обґрунтованого рішення зазвичай доводиться використовувати кілька методів. Тому результат, отриманий МАІ, перевіряють іншими методами.

Після цього оцінюють наслідки прийняття рішення ‑ як позитивні, так і негативні, маючи на увазі економію (або додаткові витрати) грошей, часу, зусиль і т.д. на виконання функції (досягнення мети).

Дата добавления: 2015-09-01