Предельные размеры обнажений пород в очистных выработках.

Устойчивость подрабатываемых горных пород, в принципе, зависит от их строения, деформационно-прочностных свойств и действующих нагрузок. Это в полной мере правомерно и для кровли камер. При этом необходимо учитывать, что массив пород в кровле камер находится в сложном и неоднородном напряженном состоянии.

При разработке месторождений полезных ископаемых лимитирующим элементом часто является кровля выработок, поскольку именно здесь, в первую очередь, возможно образование областей растягивающих напряжений, к которым особенно чувствительны массивы горных пород вследствие своих структурных особенностей и деформационно-прочностных свойств. Наряду с этим в кровле очистных выработок, особенно в областях, примыкающих к целикам, могут образовываться зоны действия высоких сжимающих напряжений. Это может иметь место, когда очистные выработки располагаются в однородных или близких по деформационно-прочностным характеристикам породах, и при этом целики полностью сохраняют сцепление с массивом пород по своим основаниям.

Таким образом, задача об определении параметров устойчивых очистных выработок может быть сведена к нахождению размеров предельных обнажении пород в кровле выработок.

В основе определения предельных размеров обнажении пород лежат предрасчеты напряженно-деформированного состояния пород вокруг очистных выработок и сравнение их с соответствующими критериями. В качестве таких критериев могут быть приняты либо деформации и напряжения, либо размеры областей или зон, где проявляются, концентрируются опасные деформации и напряжения.

В зависимости от структурных особенностей массива устойчивые параметры обнажений пород в кровле определяются различными способами.

В частности, при однородных трещиноватых породах пролет камеры будет устойчивым, если в кровле образуется свод естественного равновесия.

[Из книг: Н.З. Галаева Управление состоянием массива горных пород при подземной разработке рудных месторождений. М. Недра, 1990,177 с.

Н.З. Галаева Управление состоянием массива горных пород при подземной разработке рудных месторождений.. Учебное пособие. Л. Изд. ЛГИ, 1979. 100 с.]

Теоретические основы сводообразования в однородных горных породах впервые были разработаны профессором Рижского политехникума В. Риттером в 1879 году. Было установлено, что породы над выработкой отделяются как единое целое в форме свода, благодаря появляющимся и них растягивающим напряжениям, превосходящим предел прочности материала на разрыв. В породах, обладающих сцеплением, над выработкой образуется свод, отделяющийся по кривой АСВ (рис. 16.2) вследствие преодоления

Рис. 16.2. Расчётная схема образования свода по В. Риттеру.

усилия MN = [σ_р] ds, направленного нормально к поверхности свода (где [σ_р] - предел прочности на разрыв; ds - элементарный участок дуги). Вес пород в своде давления определяется из выражения

2a

Q = γ∫ y dx. (16.1)

Учитывая, что вертикальная составляющая сопротивления разрыву

МК = [σ_р] ds /соs α, общее сопротивление разрыву по поверхности свода будет

2a 2a

F = ∫[σ_р] ds /соs α =∫ [σ_р] [1 + (y’)²] dx. (16.2)

0 0

Здесь y’ – первая производная у по х.

Сводообразование возможно, если Q> F, т.е. когда в своде давления (обрушения) действует сила

2a 2a

Р = Q – F = γ∫ y dx - ∫ [σ_р] [1 + (y’)²] dx (16.3)

0 0

Исследуя выражение (16.3), т. е. вариацию Р по y, можно убедиться, что кривая свода представляет собой параболу

y = x γ (2a – x)/4[σ_р] (16.4)

с высотой b = a² γ/4[σ_р] при x = а (здесь а – полупролёт камеры).

При Q = F можно определить ширину выработки, при которой свод давления не образуется, и породы кровли не будут давить на крепь выработки (условие предельного равновесия). Такое условие, по В. Риттеру, соблюдается, если 2а ≤7[σ_р]/ γ.

Из теории В. Риттера следует, что своды образуются в выработках, пройденных в однородных породах, при определенных соотношениях удельного веса пород, прочности пород на разрыв и величины пролета выработки (камеры). Свод отрывается от массива в виде сплошного тела.

Проф. М. М. Протодьяконов на основании анализа предыдущих работ по исследованию механизма сводообразования пород и большого объема собственных исследований разработал теорию сводообразования более детально.

М. М. Протодьяконов рассматривал горные породы как дискретную среду, обладающую не только трением, но и сцеплением (зацеплением), при определении сопротивления сдвигу рекомендовал пользоваться «кажущимся коэффициентом трения»

f’ = (f σ + c)/σ,

где σ – нормальное напряжение; c – сцепление; f – коэффициент трения.

Согласно расчетной схеме Протодьяконов (см. рис. 16.3) на любую левую часть

Рис. 16.3 Расчётная схема образования свода по М.М Протодьяконову.

свода действуют силы горизонтальной реакции правой части свода Т, равнодействующей вертикального давления рх и реакции нижней части свода W. Равновесие рассматриваемого участка свода МО относительно точки М, координаты которой равны х и y, обеспечивается при условии

рх²/2 = Т_y, (16.5)

что свидетельствует о параболической форме свода.

В опоре свода А действуют нормальная (прижимающая) сила Р и горизонтальная (сдвигающая) сила Q. - Отношение Q / Р = tgφ = f определяет устойчивость свода. Если Q ≤ f Р, то свод будет устойчив, при Q > f Р - произойдет его разрушение.

Принимая во внимание, что Р = ра и Т = Q условие устойчивости Q ≤ f Р можно записать в виде Т '≤или Т + τb = fра (где τ - горизонтальное сдвигающее усилие на единицу вертикальной проекции свода; b — высота свода). Отсюда

Т ' = fра - τb (16.6)

Подставляя (6) в выражение (5) в точке 0 (х=а; y=b) получим усилие

ра ²/2 = (fра - τb) b, (16.7)

откуда после преобразований имеем

τ = pа(2fb – а)/ (2b²). (16.8)

Условие максимальной устойчивости будет обеспечиваться в том случае, если

τ = τ_max,. т.е.

d τ

--- = pа(a -bf)/ (b³) = 0 (16.9)

d b

Отсюда высота свода

b = a / f (16.10)

Подставив это значение b в выражение (8)

τ = pf²/2 (16.11)

Принимая во внимание выражение (5.6) можно найти величину

Т= f рa/2, (16.12)

а из (5) можно получить уравнение кривой свода, которая представляет собой параболу

у = х²/(а f). (16.13)

Выражения (16.10) и (16.13) для практических расчетов параметров сводов и устойчивых пролетов камер используются чаще всего.

Зная площадь параболического свода S = 4 аb/3, можно определить вес породы на единицу длины выработки и, следовательно, давление на крепь:

Р = γ S = 4/3 (γаb) (16.14)

Подставляя значение b = а/ f,

Р = (4/3 γа²)/ f. (16.15)

Здесь – коэффициент крепости по шкале М.М. Протодьяконова f = [σ_сж]/100;

для сыпучих и рыхлых пород f = tgφ (φ – угол естественного откоса);

для твёрдых горных пород f = tgρ (ρ – угол внутреннего трения).

Из выражений (16.14) и (16.15) следует, что давление на крепь не зависит от глубины работ. Исследования же показывают, что до глубины Н = 10а давление на крепь возрастает, а затем снижается и остается постоянным. Поэтому при небольших глубинах расчеты по формулам М.М. Протодьяконова неприемлемы. Следует отметить, что в расчетах давлений на крепь никак не учитываются характеристики крепи и время взаимодействия системы «порода — крепь».

Если же камеры остаются незакрепленными, то по теории М.М. Протодьяконова можно определить устойчивые пролеты камер с параболической формой свода. Высота свода, как свидетельствует формула (16.10), определяется прочностными параметрами пород и шириной камеры.

Предложены эмпирические формулы определения высоты подъёма свода:

По А.А. Борисову [Борисов А.А. Расчёты горного давления в лавах пологих пластов. М, Недра, 1964] для слоистых осадочных пород b = (0.21-0.30) l, где l – пролёт выработки.

По данным Н.З. Галахова для однородных трещиноватых пород b = (0.55-0.65) l.

Р. Квапил [Вопросы теории горного давления. М, Госгортехиздат, 1961] предлагает различные эмпирические формулы для сводов в зависимости от [σ_сж], ρ, γ и Н – глубины работ.

Не все исследователи считают форму свода параболической.

По С. Ирвингу (1946), образующийся над выработкой свод имеет форму полуокружности. В этом случае вес пород внутри свода

Q = π a² γ/2, где a – полупролёт выработки, γ – удельный вес пород.

По Ф. Мору(1956) и Коммерелю (1912) образующийся над выработкой свод имеет форму полуэллипса. В этом случае вес пород внутри свода

Q = π a b γ, где a,b – соответственно полупролёт выработки и высота свода (малая и большие полуоси эллипса).

На практике форма свода может значительно отклоняться от идеальной. В частности, если породы кровли имеют слоистое строение, вывалы из кровли по своей форме могут напоминать треугольники или трапеции.

Величина предельного пролёта горизонтального обнажения пород в кровле очистных камер в нетрещиноватых однородных породах может быть вычислена, исходя из параметров свода обрушения над выработкой, по формуле [Фисенко Г.Л. Предельные состояния горных пород вокруг выработок – М.: Недра, 1976]

5[ σ _р]

l _пр = ----------,(16.16)

2 γ

где [ σ _р] – предел прочности пород на растяжение, МПа; γ – плотность пород в кровле, т/м³.

В случае трещиноватых пород величина предельного пролёта горизонтального обнажения пород в кровле очистных камер вычисляется с учётом коэффициента структурного ослабления трещиноватого массива λ:

5[ σ _р]

l _пр = ---------- λ.(16.17)

2 γ

В формулах (16.16) и (16.17) в качестве параметра используется только предел прочности пород на растяжение, т. е. учитывается только один из возможных видов разрушения — отрыв при действии растягивающих напряжений.

Для расчета пролетов камер, кровля которых представлена слоистыми породами, обычно пользуются методами строительной механики, используют теорию балок и плит.

Гипотеза балок была предложена Шульцем (1867). Согласно этой гипотезе, слоистая кровля выработок рассматривается как пачка балок, заделанных или свободно опёртых по обеим сторонам выработки, на которую действует равномерно-распределённая нагрузка.

Такой подход был, в частности, разработан профессором В. Д. Слесаревым [Слесарев В.Д. Крепление подземных выработок. – М.: Гостоптехиздат, 1940.].

При этом в основу подхода В.Д. Слесарева положено понятие об эквивалентном предельном пролете, под которым подразумевается ширина выработки неограниченной длины, устойчивость которой эквивалентна устойчивости кровли выработки произвольной формы. Другими словами, В.Д. Слесарев сделал попытку устойчивость изометрической выработки весьма сложных неправильных очертаний привести к устойчивости протяжённой выработки с одним единственным параметром – шириной – пролётом.

[Из книги Н.З. Галаева Управление состоянием массива горных пород при подземной разработке рудных месторождений. М. Недра, 1990,177 с.]

Слоистуюкровлю камеры можно рассматривать как плиту, свободно опертую или защемленную по контуру выработки. Если длина камеры превышает ее ширину в три и более раз, то участок выреза пород поперек камеры рассматривается как балка-стенка, на которую действует равномерно распределенная нагрузка. Для учета граничных условий в направлении длины камеры истинный пролет камеры заменяется эквивалентным пролетом. Для расчетов предельных пролетов камер применяются методы строительной механики, рассматривающие слоистую толщу кровли камеры как упруго-пластическую среду.

Расчеты слоистой кровли камер по теории В.Д Слесарева выполняются при следующих допущениях:

· обнаженная кровля выработки подобна свободно опертой или защемленной плите;

· расчет плиты можно заменить расчетом эквивалентной балки;

· плиты и балка будут испытывать приблизительно одинаковое напряженно-деформированное состояние в наиболее опасных сечениях, если их гидравлические радиусы равны;

· всякую выработку, ограниченную по контуру, можно заменить эквивалентной выработкой бесконечно большой длины, кровля которой будет испытывать такие же напряжения идеформации, как и кровля камеры;

· для расчета однопролетной балки, эквивалентной кровле горной выработки, можно использовать графический способ построения кривой давления, который применяется в статике сооружения для расчета сводов;

· кровля горных выработок работает за пределами упругих и упруго-пластических деформаций (до момента потери его устойчивости).

Для замены в расчётах плиты эквивалентной балкой определим гидравлический радиус выработки бесконечно большой длины.

Под гидравлическим радиусом понимается отношение площади обнажении камеры S к ее периметру Р, т.е.

S ab

R = ---- = ---------, (16.18)

Р 2(a + b)

где a и b соответственно ширина и длина камеры.

При b ∞ гидравлический радиус будет стремиться

ab

lim R = lim ---------- = a/2 (16.19)

b ∞ 2(a + b)

Отсюда следует, что пролет a выработки, эквивалентнойрассматриваемойкамере l _экв = 2 R или

l _экв = 2 R = ab/(a + b ) (16.20)

При этом критерием устойчивости обнажения принимается неравенство

L ≤ l _пр,(16.21)

где l _пр предельный перед обрушением пролёт выработки с эквивалентным пролётом, т.е. неограниченной длины, определяемый расчётным или опытным путём.

Такой подход завоевал большую популярность, был оправдан достаточной простотой и наглядностью, он давал достаточно приемлемые с точки зрения практики результаты, в частности, для пластовых месторождений, где структурные неоднородности выражены, главным образом, контактами по слоям. В силу этой же особенности в подходах В. Д. Слесарева учитывается, как правило, только один из возможных видов разрушения — отрыв.

На основе изложенного подхода были предложены различные эмпирические формулы для разнообразных горно-геологических условий.

Считается, что в случае слоистого строения пород пролет камеры будет надежно устойчивым, если слои непосредственной кровли испытывают только упругие деформации, т.е. ширина камеры не превышает величины первого предельного пролета по В.Д. Слесареву. Несущая способность слоистой кровли частично сохраняется и в запредельном состоянии пород, когда посередине пролета камеры и у целиков появляются трещины разрыва — ширина камеры соответствует второму предельному пролету.

Работу кровли В-Д- Слесарев предлагает рассматривать в трех состояниях, которые он назвал предельными (табл. 16.1).

Предельные состояния слоистой кровли

Таблица 16.1

Предель-ное состояние кровли	Характеристика состояния кровли	Предельные пролёты балки
Свободно опёртой	С защемлёнными концами
I	В кровле отсутствуют растягивающие напряжения	LI = 1.15 √[σp] h/γ	LI = 1.41 √[σp] h/γ
II	Породы кровли испытывают максимальные деформации (прогиб) без нарушения сплошности Появляются трещины и возможно частичное обрушение	LII = 1.41 √[σp] h/γ     LII^’ = 1.63 √[σp] h/γ	LII = 1.73 √[σp] h/γ     LII^’ = 2.00 √[σp] h/γ
III	Трещины распространяются на всю мощность кровли, и она обрушается	LIII = 2.00 √[σp] h/γ	LIII = 2.44 √[σp] h/γ

ВеличиныL_I, L_II, L_II^’, L_III — можно принимать как предельные пролетыкровли камеры, где [σ_p] — предел прочности горной породы на разрыв кПа; h - толщина балки, м; γ - удельный вес породы, кг/м³.

Исходя из предельных пролётов по формуле (16.20) можно определить размеры камер, при которых обеспечиваются соответствующие состояния пород.

[Из книги Н.З. Галаева «Управление состоянием массива горных пород при подземной разработке рудных месторождений.». Учебное пособие. Л. Изд. ЛГИ, 1979. 100 с.]

Если массивы сложены из отдельных частиц (кусков) пород, то их можно считать дискретным материалом с малым сцеплением и применять к ним законы статики сыпучих сред. К таким породам можно отнести рыхлые осадочные и раздробленные (разрушенные) скальные породы.

Для описания поведения этих пород и определения нагрузок на крепь выработок, бокового давления закладочного материала на целики, давления обрушенных пород на днища блоков и т.д. часто пользуются расчётными методами механики грунтов.

Считается, что при неглубоком расположении выработки, вертикальное давление на её кровлю определяется весом всего столба пород, т. е. σ_z = γH, а боковое давление на стенки выработки σ_x = γH tg²(90⁰ -)/2 = γH (1 – sinρ) (1 + sinρ). Однако для больших глубин это предположение неверно, т. к., фактически, это выражения для действующих напряжений в массиве сыпучих пород. В то же время нагрузки на кровлю выработки будут совсем другими, т. к. необходимо учесть силы трения между некоторым выделенным столбом пород над выработкой и окружающим массивом.

Для определения давления с учётом указанных сил трения широко используются теории Д. Янсена (1895) и Бирбаумера (1913).

В теории Янсена определяется давление вертикального столба сыпучего материала на какую-либо горизонтальную плоскость.

При этом равновесие элементарного слоя сыпучей среды толщиной dz в любой плоскости сечения столба на глубине z определяется условием равенства действующих на этот слой сдвигающих и удерживающих сил (рис. 16.4):

Рис. 16.4. Расчётная схема для определения давления сыпучего материала (по Янсену)

σ_z F + γ F dz = (σ_z + dσ_z) F + σ_x U dz f, (16.22)

где σ_z F – давление вышележащих слоёв; F – площадь слоя; σ_z = γ z; dσ_z – давление, создаваемое элементарным слоем dz; σ_x – горизонтальный распор; U – периметр поперечного сечения столба; f – коэффициент трения.

Обозначив f σ_{x /} σ_z = K и разделив каждый член выражения (16.22) на F, после алгебраических преобразований получим

U

dσ_z / (1 – К------ σ_z) = γ dz.

γ F

После интегрирования получаем

U U

ln ((1 – К------ σ_z) = - K----- z.

γ F F

Отсюда вертикальное давление сыпучего материала на любой высоте z:

γ F

σ_z = ------- (1 – e^-K(U/F)z) (16.23)

KU

Принимая во внимание, что σ_х = К σ_z/f, можно найти

γ F

σ_х = ------- (1 – e^-K(U/F)z) (16.24)

f U

По теории Бирбаумера область влияния выработки в кровле имеет в сечении вид трапеции, при этом непосредственно на кровлю выработки действует вес столба пород Q (рис. 16.5), удерживаемый силами трения F, т. е. итоговая действующая сила

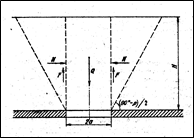
Рис. 16.5. Расчётная схема к теории Бирбаумера.

Р = Q - 2 F = Q - 2 N tgρ, (16.25)

где Q = 2а l γH; а и l – половина ширины и длина выработки.

Предполагается, что величина N обусловлена весом пород в пределах треугольной призмы, одно из рёбер которой наклонено к горизонту под углом (90⁰ - ρ)/2.

N = 0.5 γH² l tg²(90⁰ - ρ)/2; ρ – угол внутреннего трения.

Подставив значения Q и N в равенство (16.25) и преобразовав его, получим

H

Р = 2а l γH [1 - ----- tgρ tg²(90⁰ - ρ)/2]. (16.26)

2а

Поскольку Р не может быть отрицательна, должно соблюдаться условие

H

[1 - ----- tgρ tg²(90⁰ - ρ)/2]> 0

2а

Отсюда формула (16.25) справедлива при

2а

Н ≤ ----------------------.

tgρ tg²(90⁰ - ρ)/2

Напряженно-деформированное состояние обнажений камер в залежах наклонного и крутого падения определяется совместным влиянием нормальных и касательных напряжений, возникающих в результате действия гравитационных и тектонических сил. Устойчивость боков и кровли камер зависит от строения и прочности пород, глубины работ, времени существования камер и других причин. Здесь также часто применяются методы определения устойчивых параметров обнажений через величины предельных пролётов.

Например, для условий железорудных месторождений Кривого Рога [Инструкция по определению геометрических параметров этажно-камерных систем разработки в Криворожском железорудном бассейне. Кривой Рог: изд. НИГРИ, 1973.] было установлено, что предельный эквивалентный пролет наклонного обнажения пород в камерах составляет:

a b

l _пр.н = ----------,(16.27)

√ a² + b²

где a, b – соответственно размеры камер по простиранию и падению залежи, м.

[Из книги Н.З. Галаева Управление состоянием массива горных пород при подземной разработке рудных месторождений. М. Недра, 1990,177 с.]

При наклонном падении залежей или пластов, если висячий бок представлен слоистыми породами, то для определения предельного пролета обнажения применяют методы расчета свободно опертых или защемлённых по контуру тонких плит (пластин). При этом в расчетах, как правило, плитообразную кровлю заменяют балкой с эквивалентным пролетом.

Предельный пролет балки, наклоненной под углом а (угол падения рудного тела) предлагается определять по формуле

h² 2 h[σ_p] h

L_пр = ξ√----- tg² α + ---------- - -----.tg α, (16.28)

4 γ cos α 2

где ξ – коэффициент ползучести, учитывающий влияние времени на устойчивость пород висячего бока (ξ = 0.7 - 0.9); h – мощность слоя непосредственной кровли; [σ_p] – предел прочности горной породы на растяжение; γ – удельный вес пород кровли.

На практике образование зоны растягивающих напряжений, а, следовательно, и области возможного разрушения кровли в результате отрыва пород предотвращают, оформляя кровлю очистных камер в виде свода.

На основании исследования закономерностей распределения полей напряжений и параметров зон растягивающих напряжений вокруг отверстий прямоугольной формы поперечного сечения с различным соотношением высоты и ширины, параметры свода для камер с отношением высоты (h) к пролету (l) до 1/10 приближенно можно устанавливать из условия

b 1 1

----- = ----- ¸----- (16.29)

l 4 5

где b —стрела подъема свода; l —пролет очистной выработки.

Вместе с тем в реальных условиях разрушения в массивах горных пород происходят и при действии сжимающих напряжений в форме сдвига или скола, в первую очередь, по контактам структурных неоднородностей того или иного порядка.

Для учета этого вида разрушения — сдвига, особенно характерного для массивов пород блочной структуры, можно использовать условия [(3.8), тема 3], которые применяют при расчете параметров зон нарушенных пород вокруг капитальных и подготовительных выработок. Применимость этих условий к очистным выработкам подтверждается натурными наблюдениями за состоянием приконтурной области массива пород вокруг очистных выработок.

Инструментальными измерениями установлено, что вокруг очистных выработок, как и вокруг подготовительных, образуется зона нарушенных пород, в пределах которой наблюдаются раскрытые трещины и частично нарушается связь между структурными блоками. В результате создается реальная опасность вывалов пород. Для скальных массивов предельный безопасный размер зоны нарушенных пород от контура очистной выработки в глубь массива составляет 0,4 м.

Рассчитывая размеры зоны нарушенных пород по формулам (3.8) и сравнивая расчетные значения с предельными безопасными, оценивают устойчивость очистных выработок. Если расчетные значения превышают критические, следует предусматривать специальные мероприятия по обеспечению устойчивости выработок — уменьшение площади обнажения пород путем оставления целиков, путём изменения размеров и конфигурации очистных камер или возведение крепи.

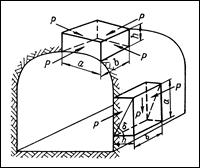
Глубиной распространения зоны нарушенных пород от контура выработок в сторону массива определяются также размеры возможных вывалов из кровли, в частности их высота (рис 16.6).

Рис 16.6. Схема действия сил на структурный блок в кровле и стенке выработки после реализации скола по поверхностям структурных неоднородностей - граням выделенных структурных блоков

Однако для условий очистных выработок проводить оценку устойчивости только по параметрам зоны нарушенных пород недостаточно, поскольку вследствие больших площадей обнажения пород в них возможны вывалы и обрушения блоков плитообразной формы. В этих случаях при незначительной высоте вывалов поперечные размеры их в плане могут быть очень велики. Подобные обрушения весьма опасны, так как помимо непосредственной угрозы людям они могут вызывать разрушительные воздушные волны и создавать опасные напряжения в массиве от удара обрушившихся масс. Вследствие этого при определении размеров предельных обнажений в очистных выработках необходимо задаваться не только критическим размером зоны нарушенных пород, но и максимально допустимыми линейными размерами (в плане) отдельных вывалов и обрушений.

Линейные размеры вывалов (в плане) находятся в определенной взаимосвязи между собой и, кроме того, определяются соотношениями объемного веса пород, напряжений распора структурных блоков и коэффициентов трения по контактам структурных неоднородностей, ограничивающих эти структурные блоки.

Эти соотношения в первом приближении могут быть выражены следующим условием образования вывалов:

g 1 1

--------³ ------ + --------, (16.30)

2 f₀ P a b

где а и b — поперечные размеры возможных вывалов или обрушений (в плане); Р—распор структурных блоков; fo—коэффициент трения по поверхностям структурных неоднородностей, g - объёмный вес пород.

Это неравенство в системе координат (а, b) представляет собой гиперболическую кривую, разграничивающую области устойчивых и неустойчивых обнажении.

Из параметров, входящих в зависимость (16.30), наиболее трудно определяются коэффициенты трения по поверхностям структурных неоднородностей и напряжения распора структурных блоков в пределах зоны нарушенных пород.

Экспериментальные данные о коэффициентах трения по поверхностям структурных неоднородностей практически отсутствуют. Имеющиеся единичные результаты определения коэффициентов трения для некоторых разновидностей руд и пород приведены в табл. 16.2.

Коэффициенты трения некоторых горных пород и руд.

Таблица 16.2

Тип пород (руды)	Коэффициенты трения
	движения	покоя
Пятнистая апатитовая руда	0.33	0.46
Рисчоррит	0.15	0.33
Сфеновый ийолит	0.26	0.38
Ийолит-уртит	0.25	0.47
Мончикит	0.19	0.38
Луяврит	0.25	0.53

Из табл. 16.2 следует, что значения коэффициента трения движения для указанных пород колеблются в пределах 0,15 — 0,33, а коэффициента трения покоя — в пределах 0,33 — 0,47. Очевидно, для расчетов целесообразнее использовать коэффициенты трения движения с тем, чтобы возможная погрешность шла в запас прочности.

Распор структурных блоков Р пока не представляется возможным надежно измерять в натурных условиях. Однако можно предположить, что верхний его предел можно установить, исходя из горизонтальных напряжений в кровле очистных выработок, если бы зона нарушенных пород отсутствовала. При таком предположении распор структурных блоков можно приближенно оценивать по результатам аналитических определений напряженно-деформированного состояния массива вокруг очистных выработок. Распор структурных блоков может также устанавливаться и методом обратных расчетов, если в условиях (16.30) известны (например, из натурных наблюдений за устойчивостью выработок) размеры отдельных вывалов.

Вполне очевидно, что при увеличении распора Р структурных блоков или коэффициентов трения f_o по поверхности структурных неоднородностей размеры устойчивых обнажении возрастают.

На рис 16.7 приведена диаграмма устойчивых обнажений кровли очистных выработок в зависимости от напряжений бокового распора структурных блоков Р и коэффициента трения f_o по поверхностям структурных неоднородностей. Значение объемного веса g ввиду его сравнительно малой изменчивости для массивов скальных пород принято постоянным (g =3,0 тс/м³).

Рис 16.7. Области устойчивых обнажении кровли выработок при различных значениях удельной силы трения.

Из диаграммы следует, например, что если произведение Pf_o = l, то предельные размеры устойчивых обнажении a х b составляют всего лишь 2х1 м (точка А); 3х0,8 м (точка Б) и т. п. Если произведение Pf_o =10, то предельные размеры устойчивых обнажении возрастают до 13,5х13,5 м (точка В); 20х10 м (точка Г) и т. п.

Во многих случаях непосредственную опасность могут представлять вывалы пород и из стенок выработок, особенно для условий большепролетных подземных сооружений типа машинных залов гидроэлектростанций, туннелей и т. д. При этом, в отличие от кровли, размеры вывалов из стенок выработок определяются лишь одним параметром — размером вывала вдоль выработки, но в предположении наличия горизонтальных естественных трещин, по которым возможен отрыв выпадающего блока.

Аналитически это выражается формулой:

g sin d 1

------ --³ ----, (16.31)

2 f₀ P b

где d - угол наклона плоскостей эффективных структурных неоднородностей (в частном случае, углы падения естественных крупноблоковых трещин для очистных выработок или подземных сооружений)

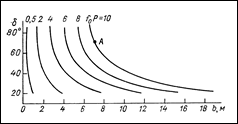
На рис. 16.8 представлена диаграмма для определения размеров возможных вывалов из стенок большепролетных выработок при различных значениях углов наклона d, структурных неоднородностей, по которым происходит скольжение вывала.

Рис. 16.8. Диаграмма для определения размеров возможных вывалов b из стенок большепролетных выработок при различных значениях углов наклона плоскостей скольжения d и силы трения.

Графическое представление предельных размеров устойчивых обнажений пород в выработках в виде некоторого семейства кривых было впервые предложено профессором Г. А Крупенниковым в 1952 г при изучении устойчивости выработок в условиях Подмосковного бассейна. При этом устойчивость выработок Г. А. Крупенников оценивал по смещениям кровли и к устойчивым обнажениям относил обнажения, при которых не происходило обрушений пород в течение определенного, заданного условиями технологии выемки угля, периода времени.

Аналогичным образом можно приближенно устанавливать параметры устойчивых обнажений по результатам визуального обследования.

На рис 16.9 в качестве примера приведена диаграмма устойчивых обнажений, построенная по данным визуальных обследований выработок на одном из медноникелевых месторождений Кольского полуострова, где разрабатывалась свита вертикальных маломощных жил системой с открытым очистным пространством и распорной деревянной крепью. При этом все обнажения пород на месторождении с некоторой условностью относили к одному из следующих трех случаев:

видимые нарушения пород отсутствуют, обнажение считалось устойчивым;

проявления горного давления слабые: это выражалось в раскрытии отдельных небольших трещин в боковых породах, в образовании небольших заколов на локальных участках выработок, в изгибании или поломке отдельных элементов крепи в очистных блоках;

проявления горного давления весьма интенсивные: ярко выраженные заколы по обеим стенкам штреков, изгиб и поломка крепи в блоках, обрушение и завал штреков.

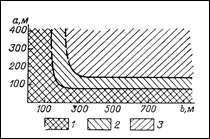
Рис. 16.9. Диаграмма устойчивости обнажении пород по результатам визуальных обследований (рудник Ниттис-Кумужье, Кольский полуостров).

Область: 1 - устойчивых обнажений, 2 - слабых проявлений горного давления, 3 - интенсивных проявлений горного давления.

На осях координат указаны размеры выработанного пространства по падению а и по простиранию б.

Кроме рассмотренных, известны способы расчета устойчивых обнажений кровли очистных выработок на основе определения разрушающих нагрузок.

При этом, выполняя расчеты устойчивости кровли камер по разрушающим нагрузкам, следует вводить в расчетные размеры необходимый коэффициент запаса, обеспечивающий надежность использования расчетных параметров. Однако в настоящее время отсутствуют обоснованные рекомендации по выбору оптимального коэффициента запаса, обеспечивающего как безопасность ведения горных работ, так и экономичность инженерных решений. На практике коэффициент запаса принимают обычно равным 2 — 3, а для особо ответственных случаев и больше.

Помимо рассмотренных основных факторов, определяющих устойчивость пород в выработках, предельные размеры обнажении зависят также и от ряда других факторов, учет которых может представлять иногда существенные трудности. К этим факторам относятся, например, снижение деформационно-прочностных характеристик пород с течением времени, влияние взрывных работ и др. Поэтому в практике в качестве наиболее надежного способа определения параметров устойчивых обнажений широко применяют производственные эксперименты. Сущность таких экспериментов заключается в постепенном увеличении пролетов камер до предельных, устанавливаемых по критическому состоянию кровли (до первого обрушения кровли или до заданной величины ее прогиба).

Например, подобными экспериментами и практикой горных работ установлено, что на рудниках Жезказгана устойчивыми являются пролеты камер:

· если кровля представлена серыми песчаниками - 15 м;

· если кровля сложена красноцветными породами - 12¸13 м.

На Белоусовском руднике (филиал ВостокКазмедь) при разработке пологих участков залежей камерно-столбовой системой устойчивые пролеты камер по многолетнему практическому опыту (разработку Белоусовского месторождения ведут уже более 200 лет) составляют 7¸8 м.

Путем обобщения практического опыта применительно к тем или иным конкретным условиям месторождений составляются частные классификации пород по устойчивости кровли. Основой этих классификаций обычно служат качественные признаки: петрографический состав, структурные и текстурные особенности пород, глубина заложения выработок, гидрогеологические условия и др.

Так, академик АН СССР М И. Агошков подразделяет горные породы по устойчивости кровли на 5 групп:

1. Породы весьма неустойчивые, не допускающие даже незначительных обнажений в кровле и боках выработки без крепления, т. е. требующие, как правило, применения опережающей крепи.

2 Породы неустойчивые, допускающие небольшие обнажения кровли и боков, т. е. требующие поддержания непосредственно вслед за выемкой.

3 Породы средней устойчивости, допускающие обнажения на относительно большой площади, т. е не требующие поддержания их сразу вслед за выемкой.

4 Породы устойчивые, допускающие значительные обнажения и требующие поддержания только в отдельных местах или через некоторые интервалы.

5 Породы весьма устойчивые, допускающие весьма большие обнажения без крепления.

При этом М И Агошков указывает, что сразу после обнажения породы часто не проявляют признаков неустойчивости, но через некоторое время вследствие изменения свойств пород во времени и под воздействием процессов выветривания становятся непрочными и теряют устойчивость.

Классификацию пород кровли по устойчивости с учетом времени существования обнажений приводит профессор А. А. Борисов. В этой классификации породы разделены на неустойчивые, слабоустойчивые, среднеустойчивые, устойчивые и весьма устойчивые.

К неустойчивым отнесены породы, которые без крепления не дают устойчивых обнажений, т е. обрушаются вслед за подвиганием забоя. Слабоустойчивые породы сохраняют устойчивость в призабойной полосе шириной до 1 м в течение 2—3 ч. Среднеустойчивые породы обеспечивают устойчивость обнажении в призабойной полосе шириной до 2 м в течение 1 сут., устойчивые — в течение 2 сут. Весьма устойчивые породы обладают длительной устойчивостью в призабойной полосе шириной 5—6 м.

На эксплуатируемых месторождениях со стабильными горно-геологическими и горнотехническими условиями отнесение пород к той или иной группе (классу) рассмотренных классификаций больших трудностей обычно не представляет.

---

Дата добавления: 2015-09-01