К неупругому деформированию.

В случаях, когда породы, в которых проводят очистные выработки и оставляют целики, проявляют пластические и вязкие свойства, расчеты на прочность кровли выработанного пространства и целиков необходимо дополнять оценкой деформируемости и жесткости системы целик — очистная выработка — вышележащая толща. При этом необходимо, чтобы деформации всех звеньев упомянутой системы не только не превышали определенных критических значений, но и соответствовали бы друг другу. Последнее условие достигается при равенстве скоростей деформирования отдельных элементов. При анализе деформируемости системы обычно пренебрегают местной сминаемостью почвы и кровли залежи над и под целиками по сравнению с продольной деформацией (сжатием) целиков и полагают для упрощения, что продольная деформация системы кровля — целик — почва под действием веса вышележащей толщи пород определяется исключительно деформацией целика.

Однако, как известно, сжатие целиков в продольном направлении вызывает их расширение в поперечном. Поперечная деформация целиков связана с продольной соотношением

e_прод = Кe_поп,( 16.38 )

где К — коэффициент поперечного расширения.

Коэффициент поперечного расширения целиков может принимать различные значения в зависимости от свойств пород, слагающих целики, и даже превосходить единицу при возникновении в целике областей разрушения, продольных трещин и др.

Возрастание поперечной деформации целиков во времени, а также увеличение продольной деформации системы кровля — целик — почва и, как следствие этого, нарушение вышележащей толщи пород протекают одновременно, причем трудно предсказать, какой из процессов в большей степени определяет устойчивость всей системы в целом. В соответствии с этим применяют и различные методы расчета целиков, учитывающие развитие того или иного вида деформаций во времени.

Наибольшее применение для предрасчета предельных деформаций целиков находит теория ползучести горных пород. Порядок вычислений при этом аналогичен расчету деформаций ползучести вокруг выработок. За основу принимают выражения перемещений, определенные из рассмотрения упругого деформирования пород, в которых в соответствии с принципом Вольтерра — Работнова упругие постоянные Е и v заменяют соответствующими временными операторами Е и v. Конкретный вид операторов зависит от функции ядра ползучести, принятой для рассматриваемых пород.

С точки зрения последующего учета ползучести пород удобны способы расчета параметров целиков, основанные на применении методов строительной механики и позволяющие представить упругие деформации или перемещения целиков в виде элементарных выражений.

Как показывают расчеты, в результате проявления реологических свойств пород существенно изменяются во времени нагрузки, воспринимаемые отдельными целиками. При этом некоторые из целиков будут “уходить” из-под нагрузки, давление на них будет уменьшаться, в то время как другие целики, воспринимая все увеличивающееся давление, могут оказаться перегруженными. Соотношение жесткостей пород почвы, кровли и самих целиков влияет на перераспределение нагрузок и напряжений в системе целик—порода. Целики, обладающие большей жесткостью по сравнению с породами кровли и почвы или по отношению к другим целикам, будут воспринимать и большие нагрузки.

В свою очередь на жесткость пород, слагающих целики, оказывают влияние изменчивость механических свойств пород на отдельных участках месторождений, а также их структурные характеристики, особенно естественная трещиноватость.

Особую актуальность расчёты параметров целиков при их неупругом деформировании приобретают для соляных месторождений. При этом обычно методы расчета расчёта устойчивых параметров целиков основываются на натурных наблюдениях за деформированием и устойчивостью целиков и выработок.

Так, исследуя деформируемость соляных пород во времени, К.-Г. Хефер экспериментально установил зависимость между скоростью поперечного расширения ленточных целиков с отношением А/а =1—1,25 (А — ширина камеры; а — ширина целика) и расчетным давлением на них для условий калийных месторождений бассейна Южный Гарц (рис. 16.14а).

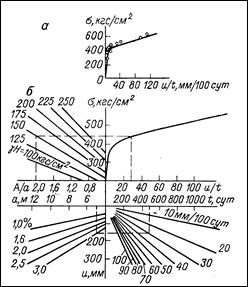
Рис 16.14. Зависимость скорости деформирования целиков от действующих напряжений в условиях соляных месторождений Южного Гарца (а) и номограмма для расчета устойчивых размеров целиков (б).

По результатам натурных наблюдений можно предрассчитать время достижения целиками предельной поперечной деформации, значение которой в зависимости от условий принимают равной (0,01—0,03) а. Для упрощения расчетов К.-Г. Хефер разработал номограмму (рис. 16.14б ).

Как и в методе К.-Г. Хефера, но только по скоростям продольных деформаций, предложил рассчитывать устойчивые параметры целиков И. А. Карманов. При этом зависимость скорости сжатия целиков от различных факторов, в том числе от действующей нагрузки, прочности пород и формы целика, а также расстояния от границ отработки определяют из натурных наблюдений за сближением кровли и почвы камер. Предельную скорость деформирования целиков устанавливают из условий устойчивости (раскрытия трещин) вышележащей толщи пород.

В методе, предложенном коллективом авторов для условий калийных и соляных рудников ОАО «Сильвинит» предлагается рассчитывать вертикальные деформации междукамерных целиков, их сжатие, которое определяет оседание водозащитной толщи и земной поверхности, а также период их весьма устойчивого состояния.

В заключение следует констатировать, что вследствие ряда трудностей, в том числе из-за отсутствия теоретического описания связи между тензором напряжений и тензором деформаций для многих пород, проявляющих реологические свойства, методы расчета целиков в условиях неупругого деформирования, разработанные на сегодня, не являются в строгом смысле теоретическими, а базируются на результатах обобщения лабораторных и натурных экспериментов с выводом эмпирических и полуэмпирических соотношений.

Дата добавления: 2015-09-01