Пример 1

Рассмотрим переходный процесс в линейной электрической цепи второго порядка, вызванный подключением источника постоянной ЭДС к последовательно соединенным сопротивлению, индуктивности и ёмкости (рис. 4.2), выбрав в качестве реакции напряжение на емкости.

Рис. 4.2

Рассмотрим переходной процесс в цепи, составив дифференциальное уравнение для искомой реакции. Поскольку цепь не содержит узлов, а представляет собой контур, то достаточно составить одно уравнение по второму закону Кирхгофа, дополнив его компонентными соотношениями:

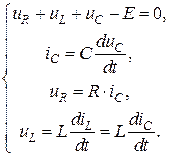(4.9)

Подставим и в первое уравнение. Получим:

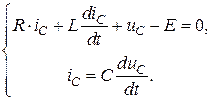(4.10)

Подстановка в первое уравнение с последующим его делением почленно на приводит к дифференциальному уравнению вида:

. (4.11)

Введем обозначения:

, .

Пусть , , , 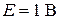. Тогда:

, .

Поскольку , то переходной процесс носит апериодический характер и свободная составляющая реакции запишется в виде:

, (4.12)

где:

,

.

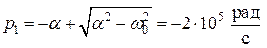Вынужденную составляющую реакции определим, исключив обе производные из дифференциального уравнения (4.11):

. (4.13)

Тогда общее решение уравнения (4.11) имеет вид:

. (4.14)

Найдем независимые и зависимые начальные условия. В момент времени источник ЭДС был отключен от цепи и, следовательно:

, .

Согласно законам коммутации:

, .

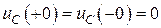Поскольку , то и .

Определим константы интегрирования и исходя из начальных условий для и . С этой целью запишем общее выражение для тока , воспользовавшись уравнение (4.13) и вторым уравнением исходной системы (4.9):

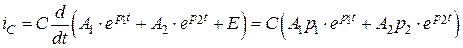. (4.15)

Подставляя начальные условия в (4.14) и (4.15) получим следующую систему для определения и :

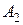(4.16)

Выразим 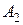из первого уравнения и подставим его во второе. Получим:

, .

Следовательно:

, . (4.17)

С учетом найденных констант интегрирования искомая реакция принимает вид:

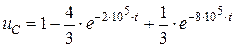. (4.18)

На рис. 4.3 представлен график зависимости найденной реакции от времени:

Рис. 4.3

Дата добавления: 2015-09-04