Краткие теоретические сведения. В отличие от рассмотренных в лабораторной работе №3 линейных электрических цепей

В отличие от рассмотренных в лабораторной работе №3 линейных электрических цепей первого порядка, переходные процессы в цепях второго порядка описываются линейными дифференциальными уравнениями второго порядка. Общий вид таких уравнений:

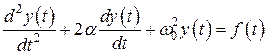, (4.1)

где 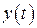- реакция электрической цепи, а - функция, определяемая задающими токами и ЭДС источников, действующих на цепь. Коэффициенты и носят названия коэффициента затухания и частоты незатухающих колебаний. Главной особенностью переходных процессов в линейных электрических цепях второго порядка является зависимость типа переходного процесса от соотношения между введенными коэффициентами, и . Различают три типа переходных процессов: апериодический, критический и колебательный. Вид свободной составляющей реакции определяется, как и в случае линейных электрических цепей первого порядка, корнями характеристического уравнения, которое в данном случае имеет вид:

. (4.2)

Вид корней этого уравнения определяется его дискриминантом.

1. Если дискриминант характеристического уравнения положителен, а это соответствует неравенству , то корни этого уравнения оказываются вещественными, разными, отрицательными. Свободная составляющая реакции цепи в этом случае определяется выражением:

, (4.3)

где . Говорят, что переходной процесс в этом случае носит апериодический характер.

2. Если дискриминант характеристического уравнения равен нулю, что выполняется при , то корни характеристического уравнения оказываются вещественными, одинаковыми, отрицательными. В этом случае свободная составляющая может быть записана в виде:

, (4.4)

где 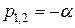. Характер переходного процесса в этом случае - критический.

3. Если дискриминант характеристического уравнения отрицателен, что возможно только при , то корни характеристического уравнения оказываются комплексно сопряженными с отрицательной вещественной частью. Общий вид свободной составляющей реакции цепи в этом случае такой же, как и для апериодического переходного процесса:

, (4.5)

где [1]. Тип переходного процесса в этом случае – колебательный.

Однако, это не единственная форма представления свободной составляющей реакции для колебательного переходного процесса. Выражение (4.5) может быть также сведено к тригонометрической форме[2]:

(4.6)

где введено обозначение .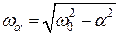

Из выражения (4.6) непосредственно виден физический смысл введенных коэффициентов. Коэффициент есть ни что иное, как относительная скорость уменьшения амплитуды колебаний. Величина описывает частоту затухающих колебаний. Если 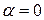, то , а значит, имеет смысл частоты незатухающих колебаний.

Помимо введенного коэффициента затухания изменение амплитуды колебаний можно характеризовать так называемыми линейным и логарифмическим декрементами затухания и . Физический смысл этих величин можно пояснить с помощью рис. 4.1, иллюстрирующего свободную составляющую реакции электрической цепи в колебательном переходном процессе.

Рис. 4.1

Под линейным декрементом затухания понимают отношение двух амплитуд свободных колебаний, отстоящих друг от друга по времени на величину периода затухающих колебаний :

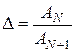. (4.7)

Из выражения (4.6) видно, что:

.

Логарифмический декремент связан с линейным декрементом затухания выражением:

. (4.8)

Простейшей цепью второго порядка является последовательное соединение источника ЭДС, сопротивления, индуктивности и емкости, известное как последовательный колебательный контур. Важнейшей характеристикой такой цепи является добротность , определяемая как отношение энергии, запасаемой в системе к энергии потерь в ней за период колебаний, умноженной на 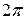. Эта величина также связана с затуханием колебаний и может быть оценена по графику свободной составляющей реакции цепи как число полных различимых колебаний.

Из выражений (4.4)-(4.7) видно, что отыскание реакции цепи сопровождается определением двух констант интегрирования ( или ). Это возможно, если известны два начальных условия, в качестве которых принято выбирать значение реакции и ее производной в момент времени .

Рассмотрим различные типы переходных процессов на конкретных примерах.

Дата добавления: 2015-09-04