Законы k - значных логик

По аналогии с алгеброй логики основные эквивалент-ности в k - значных логиках называют законами. Они отражают свойства элементарных функций.

Для операций ¦ (min, max, Å и × (умножение)) спра-ведливы свойства коммутативности:

1. ¦ (x, y) =¦ (y, x)

и ассоциативности:

2. ¦ (x, y, z) = ¦ (x,¦ (y, z)) = ¦ (¦ (x, y), z).

Для следующих пар операций ¦ и g ( a) × (умноже-ние), Å, б) min, max, в) max, min) справедлив дистрибутив-ный закон:

3. ¦ (g(x, y), z) = g(¦ (x,z),¦ (y, z)).

Для функций min, max выполняется идемпотентность:

4. min (x, x) = x, max (x, x) = x.

3.3. Функциональная полнота в Р_k

Полнота в Р_k имеет тот же смысл, что и в алгебре ло-гики. При исследовании её могут быть применены те же способы. Практическое применение критериев полноты, подобных теореме Поста, затруднено тем, что с ростом k быстро возрастает число замкнутых предполных классов в Р_k (в Р₂ их 5, в Р₃ - 18 и т.д.). Поэтому здесь необходимо разрабатывать машинные методы проверки. Реальное ис-следование полноты систем производится путем сведения их к заведомо полным либо применением специальных критериев. Полными являются, например, системы, кото-рые используются в стандартных способах представления функций.

Примеры полных систем:

1.Система Россера – Туркетта

A_{1 =} { 0, 1,..., k-1, J₀ (x),J₁ (x),...,J_{k -1}(x),min(x, y), max(x, y)} -

- используется в первой форме.

2.Система

A_{2 =} { 0, 1,..., k-1, j₀ (x), j₁ (x),..., j_{k -1}(x), x×y, xÅ y} - используется во второй форме.

3.Система Поста:

4. При простых k:

A _{4 =} { 0, 1,..., k-1, x×y, xÅ y} - используется в многочленах.

Пример. Определить, какие из констант { 0, 1,..., k-1} можно удалить в системе А₁ (Россера-Туркетта), не нару-шая её полноты.

Решение. Поскольку функции принимают значения 0 и (k - 1), то подставляя в них постоянные значения можно получить данные константы. Например: J₁(2)º0; J₁(1)º k-1.

Для практически важных систем функций разработа-ны специальные критерии полноты. Рассмотрим Р⁽¹⁾_k – множество всех функций в Р_k от одного аргумента.

Определение. Подстановками называются разнознач-

ные функции одного аргумента, принимающие все k воз-можных значений истинности. Множество всех подста-новок в Р⁽¹⁾_k обозначается через S_k.

Очевидно, подстановки задают взаимно-однозначные отображения Е _к в само себя. Множество функций одного аргумента, не являющихся разнозначными (т.е. таких, у которых имеются повторяющиеся значения истинности), обозначается через CS_k. Очевидно, что CS_k = Р⁽¹⁾_k / S_k.

Определение. Существенными называются функции Р_k, существенно зависящие от двух и более переменных и принимающие все k значений истинности.

Приведем критерии полноты функциональных систем, использующих существенные функции и функции из Р⁽¹⁾_k.

Критерий Слупецкого. Функциональная система {Р⁽¹⁾_k È f(`x)} полна в Р<sub>k</sub> при когда f(`x) – су-щественная функция.

Критерий Яблонского. Система {CS_k È f(`x)} полна в Р_k при когда - существенная функция.

Т.е. вместо всего множества одноместных функций Р⁽¹⁾_k достаточно использовать множество функций одного аргумента, не являющихся разнозначными - .

Критерий Саломаа. Система {S_k È f(`x)} полна в Р_k при k ³ 5 когда — существенная функция.

Задачи.

1. Какие из характеристических функций второго рода мож-но исключить из системы А₁, не нарушая её полноты?

2. Какие константы можно исключить из системы А₂, не нарушая её полноты?

3. Доказать полноту систем:

а) { k -1, xÅ y, max(x,y) } в (сведением к А₃);

б)) { 1, xÅ y, x 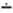y } в (сведением к А₃ , используя функ-ции ~ х, min(х, у)).

---

Дата добавления: 2015-09-04