Представление функций формулами специального вида

Будем рассматривать число значений истинности k>2, kÎ N. Множество всех значений истинности обозначим че-рез E_k = {0,1,...,k-1}. Произведением Eⁿ_k называется мно-жество всех наборов вида , где все .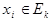

Определение. Функция 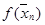называется функцией многозначной ( k -значной) логики, если `х<sup>n</sup>ÎE<sup>n</sup><sub>k</sub>, f(`хⁿ)ÎEⁿ_k.

Множество всех функций k - значной логики обозна-чается .

Определения существенных и фиктивных перемен-ных, формул, операций суперпозиции и замыкания, полно-ты имеют тот же вид, что и в алгебре логики.

Основные способы задания функций k - значной ло-гики - с помощью таблиц истинности и выражение через элементарные функции. В таблицах истинности наборы значений переменных располагаются в лексикографическом порядке, при котором векторам `х ⁿ соответствуют числа от 0 до k ⁿ - 1 в системе счисления с основанием k.

В качестве элементарных выделены следующие функ-ции:

1. Константы. Принимают значения от 0 до k -1, являются функциями произвольного числа переменных, принимаю-щими постоянные значения на всех наборах.

2. Отрицание Поста: х Å 1 (mod k). Обозначается .

3. Отрицание Лукасевича: 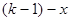. Обозначается N(x) или ~х.

4. Характеристическая функция 1-го рода :

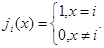
5. Характеристическая функция 2-го рода :

6. Минимум: min (x,y).

7. Максимум: max (x,y).

8. Сумма по mod k: x Å y.

9. Произведение по mod k: xy (mod k).

10. Усеченная разность:

_æ 0, x < y,

x 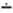y = í

è x-y, x ³ y.

11. Импликация:

12. Функция Вебба:

V _k(x,y)=max(x,y) Å 1.

13. Разность по mod k:

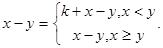
Для функций из существуют формульные выраже-ния, аналогичные нормальным формам и полиному Жегал-кина в алгебре логики.

Определение. Первой формой функции 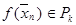яв-ляется её представление в виде:

где максимум берется по всем наборам значений перемен-ных `х ⁿ.

Определение. Второй формой функции 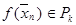является её представление в виде:

где сумма берется по всем наборам значений `х ⁿ.

Замечание. При представлении функций в первой и второй формах построение производится непосредственно по наборам переменных и значениям функции. При этом наборы, на которых f = 0, можно опускать, поскольку внут-ренние функции форм на них обращаются в нуль.

Определение. Многочленом по модулю k называется выражение вида:

Q(`x ⁿ)=a₀ Å a₁X₁ Å... Å a _mX_m,

где а X _j - произведения переменных .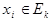

Поскольку умножение ассоциативно, то величина про-изведения х×х×...×х не зависит от порядка выполнения эле-ментарных умножений и его будем обозначать в виде степени х^s , где s - число сомножителей в произведении.

Определение. Функция f (`x <sup>n</sup>) Î P<sub>k</sub> реализуется мно-гочленом Q(`x ⁿ) по 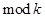, если Q(`x <sup>n</sup>) = f (`x ⁿ) при всех .

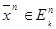В первой и второй формах функции в представимы всегда. В форме многочлена Q(`x <sup>n</sup>) по модулю k все функ-ции в представимы только тогда, когда k - простое чис-ло. Возможность представления любой функции в виде многочлена при простом k следует из того, что все степе-ни переменной х<sup>s</sup> при s = 0,..., k - 1 будут являться по-парно различными функциями. В Q(`x ⁿ) общее число по-парно различных (с точностью до перестановки сомножи-телей) произведений, содержащих степени переменных из `x <sup>n</sup> от 0 до k-1, равно числу k<sup>n</sup> всех возможных наборов переменных. Для построения Q(`xⁿ ) можно использовать

метод неопределенных коэффициентов. При составном k степени переменных х^s при s = 0,..., k-1 не будут различ-ными функциями, поэтому представление многочленами возможно не для всех функций.

Пример 1. Представить функцию f = x y ² при k =3 в первой и второй формах.

Решение. Таблица истинности функции f = x y ² имеет сле-дующий вид:

N	x	y	f
0	0	0	0
1	0	1	0
2	0	2	0
3	1	0	0
4	1	1	1
5	1	2	1
6	2	0	0
7	2	1	2
8	2	2	2

Поскольку функция принима-ет ненулевые значения только на наборах с номерами 4,5,7,8, то первую и вторую формы можно построить только по данным наборам.

Обе формы получаем путём подстановки значений перемен-ных и функции в общие форму-лы.

Первая форма принимает вид:

f=max{min(1,J₁(x),J₁(y)),min(1,J₁(x),J₂(y)),min(2,J₂(x),J₁(y)),

min(2,J₂(x),J₂(y))}.

Вторая форма:

f =j₁(x) j₁(y) Å j₁(x) j₂(y) Å 2 j₂(x) j₁(y) Å 2 j₂(x) j₂(y).

Пример 2. Представить функцию f = x É y ² при k =3 в виде многочлена по модулю 3.

Решение.

Таблица истинности функции f = xÉ y ² приведена ниже. В общем виде многочлен от двух переменных х, у, степени которых не превышают 2 (2=3-1), имеет вид:

Q = a₀ Å a₁ х Å a₂ y Å a₃ хy Å a ₄ x ² Å a ₅ y ²Å a ₆ x ²y Å a ₇ y ²xÅ a ₈x ²y ².

N	x	y	f
0	0	0	2
1	0	1	2
2	0	2	2
3	1	0	1
4	1	1	2
5	1	2	2
6	2	0	0
7	2	1	1
8	2	2	2

Последовательно подставля-ем наборы переменных с номе-рами 0 - 8 в общее выражение многочлена и определяем значе-ния коэффициентов.

0. х=0, у=0. Q = a₀ =2,Þ a₀ =2.

1. х=0, у=1. Q = 2 Å a₂ 1 + a₅ 1=2, Þ a₂ Å a ₅ =0.

2. х=0, у=2. Q = 2 Å a₂ 2Å a ₅ 1=2, Þ 2a₂ Å a ₅ =0. Из 1 и 2 следует: a₂ = 0, a ₅ = 0.

3. х=1, у=0. Q = 2 Å a₁ 1 Å a ₄ 1=1 Þ a₁ Å a ₄ =1-2=2.

4. х=1, у=1. Q=2Å a₁ 1Å a₃ 1Å a ₄ 1Å a ₆ 1Å a ₇ 1Å a ₈1=2. Þ a₁Å a₃ Å a ₄Å a ₆Å a ₇Å a ₈ =0.

5. х=1,у=2. Q=2Å a₁ 1Å a₃ 2Å a ₄ 1Å a ₆ 2Å a ₇ 1Å a ₈1=2. Þa₁Å a₃ Å a ₄Å 2a₆ Å a ₇ Å a ₈ =0.

6. х=2, у=0. Q = 2Å a₁ 2 Å a ₄ 1=0 Þ 2a₁ Å a ₄ =0 - 2=1.

Из 3 и 6 следует: a₁ = 2, a ₄ = 0.

7. х=2,у=1. Q=2Å 2×2Å a₃ 2Å a ₆ 1Å a ₇ 2Å a ₈1=1. Þ 2a₃ Å a ₆ Å 2a ₇ Å a ₈ =1.

8. х=2,у=2. Q=2Å 2×2Å a₃ 1Å a ₆ 2Å a ₇ 2Å a ₈1=2. Þ a₃ Å 2a ₆ Å 2a ₇ Å a ₈ =2.

Подставив в 4 и 5 a₁ = 2, a ₄ = 0 и объединив полученные уравнения с 7 и 8, получим следующую систему из четырёх уравнений относительно a₃ ,a ₆,a ₇ ,a ₈:

а) a₃ Å a ₆ Å a ₇ Å a ₈ =1.

б) 2a₃ Å 2a ₆ Å a ₇ Å a ₈ =1.

в) 2a₃ Å a ₆ Å 2a ₇ Å a ₈ =1.

г) a₃ Å 2a ₆ Å 2a ₇ Å a ₈ =2.

Сложив б) - г), получим: 2a₃ Å 2a ₆ Å 2a ₇ =1.

Отсюда: a₃ Å a ₆ Å a ₇ =2. Вычитая полученное уравнение из а), получим: a ₈ =2.

Подставляя a ₈ =2 в б)-г) и вычитая их из уравнения 2a₃ Å 2a ₆ Å 2a ₇ =1, получим: a ₇ =2, a ₆ =2, a₃ =1.

В итоге искомый многочлен примет вид:

f=2Å 2 х Å ху Å 2 x y ²Å 2x ²y Å 2x ²y ².

Дата добавления: 2015-09-04