Розділ iіі

Вступ до математичного аналізу

Функції однієї змінної

Змінна величина називається функцією незалежної змінної , якщо кожному значенню із деякої множини поставлено у відпо-відність єдине значення .

Якщо є функцією від , то записують .

Змінна називається аргументом функції .

Вираз 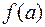означає те значення , яке приймає функція при .

Множина , що є сукупністю значень незалежної змінної , для яких визначаються значення залежної змінної , називається областю визначення функції (або областю існування).

Геометрично, область визначення функції є проекцією графіка функції на вісь .

Приклад 1. Знайти область визначення функції

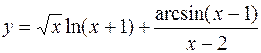
Розв’язання. Враховуючи, що

- вираз під коренем парного степеня повинен бути невід’ємним,

- вираз, що є аргументом логарифма, повинен бути додатним,

- вираз знаменника дробу не повинен дорівнювати 0,

- модуль виразу, що є аргументом арксинуса, повинен бути , маємо систему нерівностей

Отже, область визначення функції:

Сукупність значень , які відповідають всім значенням , називається областю значень (або областю зміни) функції.

Функція називається однозначною, якщо кожному значенню відповідає одне єдине значення , в протилежному випадку – многозначною.

Елементарними функціями називаються степеневі, показникові, логарифмічні, тригонометричні, обернено тригонометричні, гіперболічні функції, а також функції, що отримуються із вище перерахованих за допомогою арифметичних дій (додавання, віднімання, множення, ділення) і суперпозиції (операції взяття функції від функції), що застосовуються скінченне число разів.

Основні елементарні функції і їх графіки

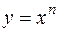
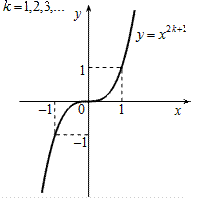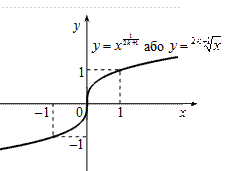Степенева функція	Рис. 1 Рис. 2 Рис. 3 Рис. 4 Рис. 5 Рис. 6
Показникова функція , Частинний випадок: експоненціальна функція	Рис. 7 Рис. 8
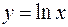
Логарифмічна функція , Частинний випадок: натуральний логарифм ()	Рис. 9 Рис. 10
Тригонометричні функції	Рис. 11 Рис. 12 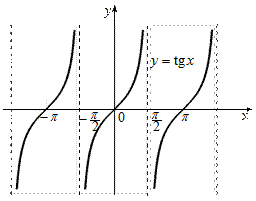Рис. 13 Рис. 14
Обернено тригонометричні функції	Рис. 15 Рис. 16 Рис. 17 Рис. 18
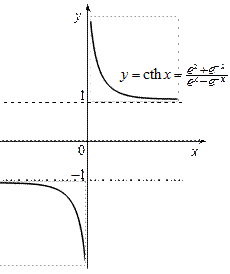Гіперболічні функції	Рис. 19 Рис. 20 Рис. 21 Рис. 22

Зауваження:

1) Графік функції отримується паралельним перенесенням графіка функції вздовж осі на величину 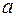у додатному напрямку при і у від’ємному напрямку при .

2) Графік функції отримується паралельним перенесенням графіка функції вздовж осі на величину у додатному напрямку при 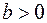і у від’ємному напрямку при .

3) Графік функції 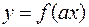, , отримується із графіка
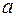функції стиском його в разів (при ) або розтягненням в разів (при ) вздовж осі .

4) Графік функції 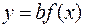, , 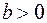отримується із графіка
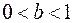функції розтягненням його в разів (при ) або стиском в разів (при ) вздовж осі .

5) Графік функції отримується симетричним відображенням графіка функції відносно осі .

6) Графік функції отримується симетричним відображенням графіка функції відносно осі .

Приклад 2. Побудувати графік функції , виді-ливши повний квадрат та перетворюючи графік .

Розв’язання. Перетворимо праву частину заданої функції наступним чином:

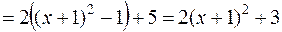Отже, задану функцію можна записати так: Графіком цієї функції є парабола, яка отримується із параболи розтягненням її вздовж осі в 2 рази і паралельним перенесенням вздовж осі на 1 одиницю вліво та вздовж осі на 3 одиниці вгору (рис. 23).

Рис. 23

Границя функції

Число називається границеюфункції при прямуючим до 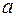(), якщо для всіх значень , які достатньо мало відрізняються від 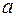, відповідні значення функції достатньо мало
відрізняються від числа , і записується це так

або при

Зауваження:

1) 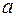– може бути скінченним числом або .

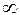2) Якщо функція має границю при , то тільки одну.

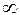3) Якщо значення функції прямують до при , то кажуть, що границею функції при є нескінченність і записують .

Функція називається нескінченно великою при , якщо

Функція називається нескінченно малою при , якщо

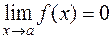
Зауваження:

1) якщо при , то при ;

2) якщо при , то при .

Властивості границі

1) ,

2)

3)

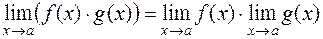
4)

5)

6)

7)

8)

Теорема. Якщо функція монотонно зростає (убуває) і обмежена зверху (знизу), то вона має границю.

Методи обчислення границь

Для безпосереднього знаходження границі , не користуючись правилом Лопіталя (див. розділ IV), у вираз під знаком границі підставляють замість його граничне значення 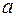і обчислюють використовуючи властивості границі та співвідношення нескінченно великих і нескінченно малих функцій.

Приклад 3. Знайти границі, не користуючись правилом Лопіталя:

1) ;

2) ;

3) .

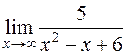Дата добавления: 2015-09-02