Розв’язання. 1)Підставляючи у заданий вираз , отримаємо

1) Підставляючи у заданий вираз , отримаємо

2) Так як безпосереднім підставленням отримуємо, що при , при , то, враховуючи співвідношення для нескінченно великих і нескінченно малих функцій, при . Отже

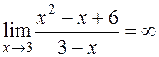
3) Безпосередньо підставляючи отримуємо, що при 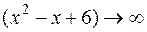, тоді при :

.

Якщо при знаходженні границі маємо, що і , то отримуємо невизначеність виду .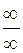

Аналогічно, з’являються інші види невизначеностей.

Види невизначеності:

; ; ; ; ; ;

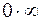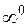
Розкриття невизначеності

Невизначеність виду може утворитись при обчисленні границі функції, у якої в чисельнику і знаменнику многочлени, при . Для розкриття цієї невизначеності треба чисельник і знаменник поділити на змінну в самому високому степені, який міститься в заданому виразі. Далі обчислюють знов, використовуючи властивості границі та властивості нескінченно великих і нескінченно малих функцій.

Приклад 4. Знайти границю, не користуючись правилом Лопіталя:

Розв’язання. Безпосереднім підставленням маємо невизначеність , тоді ділимо чисельник і знаменник на 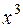. Маємо

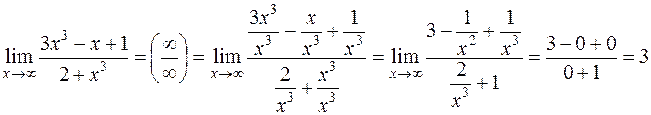Розкриття невизначеності

1) Невизначеність виду може утворитись при обчисленні границі функції, у якої в чисельнику і знаменнику многочлени, при прямуючим до якогось скінченного числа. В цьому випадку необхідно многочлени в чисельнику і в знаменнику розкласти на прості множники і скоротити.

Приклад 5. Знайти границю, не користуючись правилом Лопіталя:

Дата добавления: 2015-09-02