Основні теоретичні відомості

У класичній однофакторній лінійній регресії ми розглядали випадок коли деяка функція у залежить тільки від одного параметру х.

На практиці економічний процес змінюється під дією багатьох різних факторів, які необхідно виявити і оцінити.

Економічний процес (або явище), який залежить від більш ніж одного фактору, можна описати за допомогою багатофакторної регресії. Прикладом такої регресії можна привести залежність витрат однієї сім’ї за рік у на придбання товарів для сім’ї .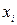

У загальному вигляді таку залежність можна записати у вигляді: 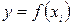, де 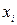– фактори.

Факторами, у наведеному прикладі можуть виступати:

– витрати на продукти харчування;

– витрати на одяг;

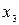– витрати на відпочинок і т.д.

У загальному випадку, якщо пропустити, що 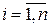, лінійна багатофакторна модель з n – змінними має вигляд:

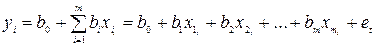(1),

де 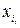– аргументи, що задані (наприклад, кількість проданого м’яса та м’ясопродуктів у t-му році на 1 особу);

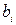– невідомі параметри моделі, які необхідно оцінити;

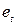– випадкова величина, яка є відхиленням від теоретичної функціональної залежності у t-му році.

Модель (1) має n – незалежних змінних (або факторів), які впливають на залежну змінну , а також n+1 параметрів 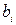, які необхідно визначити

Як і у випадку простої лінійної залежності, невідомі параметри моделі можна визначити за допомогою методу найменших квадратів (1МНК), тобто мінімізувати суму квадратів відхилень: 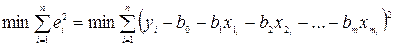(2)

Для того, щоб знайти мінімальне значення функції (2) необхідно прирівняти до нуля часткові похідні цієї функції. У результаті, після диференціювання отримаємо систему нормальних рівнянь, розв’язавши яку одержимо вирази для знаходження невідомих параметрів 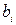, тобто:

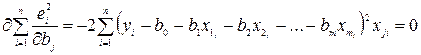(3), де .

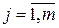Система нормальних рівнянь для функції (3) має вигляд:

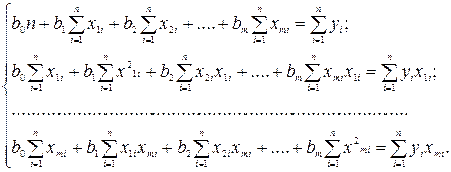(4)

Найбільш простим прикладом багатофакторної моделі є 2-х факторна модель, коли функція 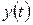залежить від двох змінних і .

Загальний вигляд лінійної 2-факторної моделі: 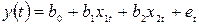(5)

Параметри моделі знайдемо, мінімізувавши суму квадратів відхилень помилок 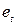, тобто прирівнявши до нуля частинні похідні виразу (5) по b. Результатом диференціювання по шуканим параметрах буде система нормальних рівнянь:

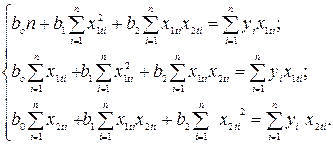(6)

За допомогою системи (6) можна легко визначити параметри та синтезувати модель виду (5).

Для перевірки адекватності багатофакторної регресії моделі використовують F-критерій Фішера з 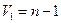, 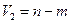ступенями вільності:

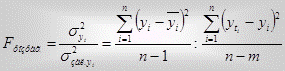(7),

де 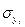– середньоквадратичне відхилення;

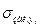– залишкове середньоквадратичне відхилення тренду, скоректоване по числу ступенів вільності;

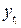– трендові рівні, розраховані по відповідній моделі;

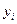– фактичні значення функції (вхідні дані);

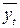– середнє трендове значення для вибраної моделі;

n – число рівнів ряду базисного ряду динаміки;

m – число параметрів відповідної моделі;

n-m – число ступенів вільності.

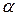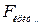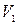Для заданого рівня значущості знаходимо для і 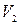ступенів вільності та порівнюємо з розрахунковими значеннями .

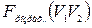Якщо 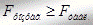, то синтезована модель є адекватною і її можна використовувати для прогнозу залежної змінної. Прогнозні значення функції одержимо шляхом підстановки в одержане рівняння значення факторів 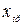або (точковий прогноз).

Значення інтервалу, в який з заданою імовірністю попадає прогнозне значення залежної змінної (напівширину довірчого інтервалу), для багатофакторної моделі розраховується за формулою: 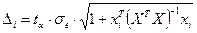(8)

де Х – матриця аргументів;

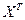– матриця, транспонована до Х;

х_і – вектор значень з п факторів у період прогнозу і;

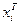– вектор, транспонований до х_і;

σ_e– середньоквадратичне відхилення похибок: σ_e = .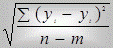

Для нашої лабораторної роботи, коли будується двофакторна модель, доцільнішим буде використання дещо спрощеної формули:

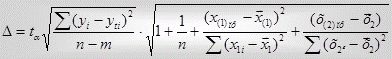(8.1),

де 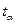- коефіцієнт Стьюдента для заданого α та n-m;

n – кількість спостережень;

m – кількість параметрів у моделі;

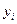– фактичні значення функції;

– теоретичні значення функції (трендові рівні);

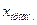– і -те прогнозне значення аргументу.

Точність прогнозу можна визначити за допомогою відностної похибки, яка розраховується за формулою: ,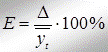

де 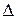– напівширина довірчого інтервалу;

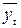– середнє трендове значення функції по обраній моделі.

Важливою є також проблема визначення степені впливу кожного аргументу на функцію. Для цього визначають коефіцієнти еластичності та -коефіцієнти. Чим більше (по модулю) значення коефіцієнтів, тим даний фактор має більший вплив на функцію. Коефіцієнти визначаються за формулами:

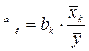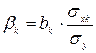; ; k=1;2 (10)

де ; .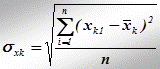

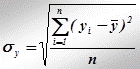При побудові багатофакторної моделі необхідно, щоб зберігалась умова незалежності між факторами. В іншому випадку кажуть, що між факторами існує колінеарність (або мультиколінеарність, коли є залежність більше ніж між двома факторами).

Одним із методів перевірки присутності колінеарності між двома факторами є визначення коефіцієнту парної кореляції.

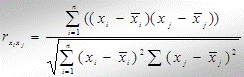(11)

Якщо коефіцієнт парної кореляції по модулю перевищує значення r = 0,8, то між факторами існує колінеарність.

Найбільш повно дослідити наявність колінеарності у масиві незалежних змінних можна за допомогою алгоритму Фаррара-Глобера (див. лекції).

Дата добавления: 2015-09-02