Теоретические сведения о зубчатых передачах

Зубчатые передачи широко применяются в машиностроении и приборостроении и служат как для понижения, так и для повышения скорости при передаче вращения от привода двигателя к исполнительному органу. Основными достоинствами передач зацепления в сравнении с другими передачами является: компактность, высокий КПД, большая долговечность и надежность в работе, отсутствие проскальзывания, применение в широком диапазоне передаваемых мощностей, высокая кинематическая точность, простота в эксплуатации. К недостаткам относят сложность в изготовлении, шум при работе.

Простейший зубчатый механизм (рис.1) состоит из двух зубчатых колес и стойки (неподвижного звена - корпуса). На колесах нарезают зубья определенного профиля на равном расстоянии один от другого, то есть с определенным шагом p. При вращении ведущего колеса его зубья взаимодействуют с находящимися в контакте (зацеплении) зубьями ведомого колеса, в результате оно тоже вращается. Поэтому зубчатая передача может передавать непрерывно вращающий (крутящий) момент сил.

Отношение угловых скоростей зубчатых колес или частот вращения передачи

называют передаточным отношением.

а б

Рис. 1. Простейшие зубчатые механизмы

Пусть зубчатый механизм передает мощность N, тогда крутящий момент на выходном валу , а на выходном , следовательно, или .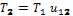

В передаче неизбежны некоторые потери мощности из-за трения, эти потери можно оценить коэффициентом полезного действия η, тогда .

При вращении зубчатых колес можно представить две касающиеся между собой окружности, которые перекатываются друг по другу без скольжения, их называют окружностями. Окружные (линейные) скорости точек начальных окружностей можно вычислить по формулам и , где r_1w и r_2w радиусы начальных окружностей.

Поскольку должно соблюдаться условие , то и передаточное отношение .

Для взаимодействия пары зубчатых колес необходимо, чтобы их шаг зацепления был одинаков, то есть , где количество зубьев взаимодействующих колес и передаточное отношение выражается следующим отношением .

Передаточное отношение при параллельных осях вращения принимается с отрицательным знаком, если входное (ведущее) и выходное (ведомое) колеса вращаются в разные стороны, и положительным, если вращение в одном направлении, что может быть обеспечено в наружном (рис. 1, а) или внутреннем (рис. 1, б) зацеплении соответственно.

Шаг p зубьев колес измеряется по дуге начальной окружности. Длина начальной окружности произвольного колеса равна , с другой стороны она равна zp, где z– число зубьев, тогда .

Отношение называется модулем зацепления. Для проектирования, изготовления и измерения параметров колес целесообразно для выбирать рациональные и целые значения. Следовательно, если m принять рациональным числом, то и значение будет рациональным. Поэтому значение модуля m как основного параметра, определяющего размер зубчатого колеса, стандартизовано. Окружность, диаметр которой выражается через модуль стандартного значения , называется делительной.

Передаточные механизмы служат для передачи движения от двигателя к исполнительному механизму. Передаточные механизмы могут состоять из различного вида зубчатых передач. В качестве передаточных механизмов могут применяться планетарные и дифференциальные механизмы.

Передаточное отношение передаточного механизма может быть найдено как отношение угловых скоростей частот вращения на входе и выходе или как произведение отдельных передаточных отношений отдельных передач , где n – число передач.

Передаточное отношение зубчатых передач (рис. 1) рекомендуется принимать .

Планетарные передачи относятся к группе эпициклических, отличительной особенностью которых является наличие в них сателлитных зубчатых колес, которые вращаются как относительно собственных осей, связанных с водилом, так и относительно центральных осей центральных колес вместе с водилом.

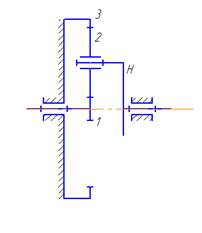
Схема 1

Рис. 2. Схемы построения планетарных передач (см. также с. 4)

Схема 2

Схема 3 Схема 4

Рис. 2. Окончание

Проектирование планетарных редукторов

При проектировании планетарных редукторов необходимо, чтобы выполнялись пять условий.

1. Кинематическое условие – редуктор должен обеспечивать требуемое передаточное отношение.

2. Условие соосности, центры вращающихся центральных колес и водила должны совпадать.

3. Условие соседства, соседние сателлиты не должны зацеплять друг друга.

4. Условие сборки.

5. Условие отсутствия интерференции или условие не заклинивания – при внешних зубьях их число должно быть больше семнадцати, то есть , при внутренних зубьях .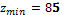

Число зубьев подбирают по первым двум условиям. Передаточное отношение редуктора по схеме должно быть больше двенадцати.

Редукторы по схеме 2 могут обеспечивать большие и очень большие передаточные отношения, хотя с ростом передаточного отношения уменьшается коэффициент полезного действия.

Рассмотрим примеры проектирования.

Такой редуктор проектируется по схеме 1. Передаточное отношение такого редуктора определяется по формуле. Выберем . Тогда , чего быть не должно согласно пятому условию (). Теперь возьмем и получим

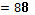, что обеспечивает выполнение пятого условия.

Число зубьев второго колеса найдем из условия соосности 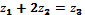, получаем .

При проектировании планетарного редуктора с передаточным отношением можно рекомендовать редуктор по схеме 2 или 3.

Для схемы 2 передаточное отношение определяется по формуле, то есть условие соосности при одинаковом модуле может быть записано .

Разложим число 28 на простые числа, чтобы было четыре сомножителя умножим и разделим полученное выражение на простое число, например 3. Тогда получим.

Число зубьев может быть найдено с помощью следующих формул

,

,

,

.

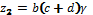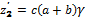В них γ какое-либо положительное число, выбор которого обусловлен выполнением пяти условий.

Пусть , , 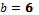, , 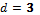следовательно,

,

,

,

.

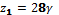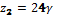Условие соосности выполняется при любом значении γ:

, γ не должно равняться 1, так как в этом случае , что противоречит условию 5.

Возьмем и будем иметь

,

,

,

.

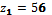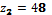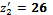Передаточное отношение редуктора, сконструированного по схеме 3, определяется по формуле и .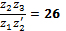

Разложим число 26 на простые числа , умножим и разделим полученное выражение на простое число 3, получим

. Условие соосности при одинаковом модуле может быть записано .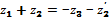

Число зубьев при этом может быть найдено с помощью следующих формул

,

,

,

.

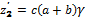Подсчеты дают 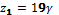, , 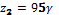, . Условие соосности выполняется при любом значении γ:

. Заметим, что при γ=1 пятое условие незаклинивания выполняется. Следовательно, окончательно получаем ,

, , .

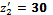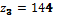Число блоков сателлитов будет определяться по условию соседства, по формуле

, так как наименьшим по размеру из сателлитов будет сателлит с числом зубьев .

В данном случае . Возможное число сателлитов 1, 2, 3, … чтобы определить окончательно, запишем условие сборки, где c – целое число. В нашем случае условие выполняется при или .

Так как обоим условиям: сборки и соседства удовлетворяет , то условие соседства не меняется.

Рассмотрим пример, когда передаточное отношение имеет очень большое значение.

Примем конструкцию редуктора по схеме 2.

Передаточное отношение определяется по формуле, формула показывает, что положительное передаточное отношение может быть по величине близким к 1, так как . Чтобы избежать больших чисел зубьев для колес, воспользуемся обратным передаточным отношением, это возможно, если сделать водило входным звеном. Пусть , Пусть , , , .

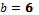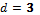Число зубьев при этом можно определить по формулам

,

,

,

.

,

,

,

.

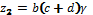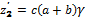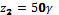Условие соосности .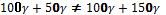

Выберем .

Дата добавления: 2015-09-01