Расчет параметров зацепления

ПРОЕКТИРОВАНИЕ КИНЕМАТИЧЕСКОЙ СХЕМЫ ПЛАНЕТАРНОГО РЕДУКТОРА И РАСЧЕТ ЭВОЛЬВЕНТНОГО ЗАЦЕПЛЕНИЯ

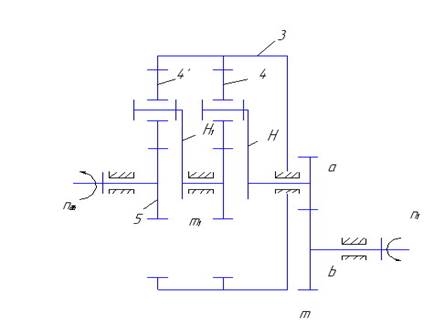
Рисунок 4.1 – Схема зубчатого механизма

Проектирование планетарного редуктора

Исходные данные:

z_а=13; z_в=18; mпл=3,5; к=4; m=5; nдв=1050 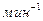; n1=45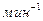

Передаточное отношение

Передаточное отношение между колесами а,в

.

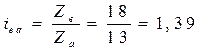Передаточное отношение в планетарной ступени

. (4.1)

Согласно [ 1,с. 35 ]

(4.2)

Где C - любое целое число.

После подстановок и перевода десятичных дробей в обыкновенные правая часть последовательно примет следующий вид:

.

Умножим правую часть отношения (1) на 40. Тогда с учетом (2) получим:

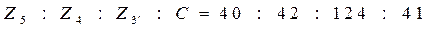. (4.3)

Отсюда , , , , ,

Проверяем условие соседства:

(4.6)

где - число сателлитов планетарного механизма

Выразим K:

Примем

Проверяем условие сборки

(4.7)

где - сумма чисел зубьев в одной из ступеней механизма

- целое число

- условие сборки выполняется

Определяем диаметры зубчатых колес планетарного редуктора

(4.4)

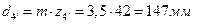
Масштабный коэффициент построения

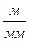
где - значение диаметра на чертеже(принимаем равным 180 мм)

Таблица 4.1 Значения диаметров зубчатых колёс на чертеже

d3 =d3^,,мм	d4 =d4^,,мм	d5= d5^,,мм	dH =dH^,,мм
		58,1	119,1

Построение плана скоростей и картины угловых скоростей и определение передаточного отношения редуктора графическим методом.

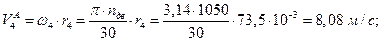
где ─ скорость точки А колеса 4, м/с;

─ угловая скорость колеса 4, с^-1;

n_дв ─ частота вращения колеса, об/мин;

Определим масштабный коэффициент плана скоростей:

;

где ─ масштабный коэффициент плана скоростей, ;

Аа ─ вектор скорости точки А колеса 4, мм.

На плане скоростей:

O₄-a ─ линия распределения скоростей колеса 4;

B-a ─ линия распределения скоростей колеса 3 (сателлита);

O₃-h ─ вектор скорости центра сателлита и верхней точки водила, мм;

А-a’ ─ вектор скорости водила на уровне колеса 4, мм;

O_H-h ─ линия распределения скоростей водила;

По плану скоростей определяем передаточное отношение редуктора:

Масштабный коэффициент картины угловых скоростей:

где ─ длина отрезка на картине угловых скоростей, мм

По картине угловых скоростей определяем передаточное отношение редуктора:

где , ─ углы между прямой отсчета и линиями распределения угловых скоростей О₄ и О_Н соответственно, град.

Расчет параметров зацепления

Исходные данные: z₁=13, z₂=18, m=5;

Коэффициент смещения:

(при z₁<17);

(при z₂>17);

где х₁, х₂ - коэффициенты смещения четвертого и пятого колеса.

Определим делительные диаметры

(4.5)

Диаметры основных окружностей:

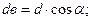(4.6)

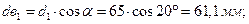
Инволюта угла зацепления:

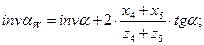(4.7)

по таблице находим

Шаг зацепления по делительной окружности:

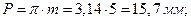
где m – модуль зубчатых колес.

Делительное межосевое расстояние

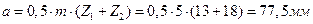
Межосевое расстояние:

Диаметры начальных окружностей:

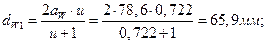
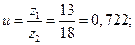
Коэффициент воспринимаемости смещения

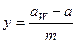
Коэффициент уравнительного смещения

Диаметры окружностей впадин:

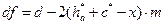(4.7)

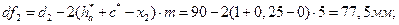
Высота зуба:

Диаметры окружностей вершин:

(4.8)

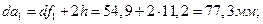
Угловой шаг зубьев

(4.9)

Углы профиля в точке на окружности вершин

(4.10)

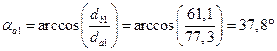
Толщина зуба по делительной окружности:

(4.11)

где 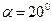- угол профиля зуба рейки.

Радиус кривизны эвольвенты на вершине зуба:

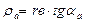(4.12)

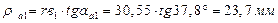
Радиус кривизны эвольвенты на впадине зуба:

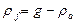(4.13)

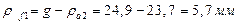
Длина линии зацепления:

Длина активной линии зацепления:

Угол перекрытия:

(4.14)

Масштабный коэффициент построения

где массштабный коэффициент эвальвентного зацепления

Полученные результаты сводим в таблицу 4.1

Таблица 4.1 - Расчетные радиусы и размеры, мм

	r	rf	ra	rb	rw	S	h	aw
		122,5	172,5	136,4	147,1	38,8		350,1
	200,1			188,8		35,3

Строим зубчатое зацепление.

Коэффициент перекрытия зубчатой передачи определяем (графически) по формуле

где, - длина активной линии зацепления

- основной шаг,

Для определения коэффициента перекрытия зубчатой передачи аналитически воспользуемся формулой:

где, - углы профиля в точке на окружности при вершине

- угол зацепления

Определим погрешность определения :

Коэффициенты удельного скольжения:

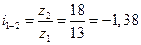
где i_1-2 ─ передаточное отношение от первого колеса ко второму;

i_2-1 ─ передаточное отношение от второго колеса к первому;

N₁N₂ ─ длина теоретической линии зацепления;

х ─ текущее значение линии N₁N₂ , взятое в сторону от меньшего колеса к большему;

Остальные значения коэффициентов удельного скольжения для соответствующих значений х занесём в таблицу 2.4:

Таблица 4.2 Значения и вектора коэффициентов удельного скольжения
	N1	a				W			b		N2
xi, мм			13,6	27,2	40,8	54,4	73,2		105,6	110,9	129,3
l1	-∞	-6,7	-6,6	-3,1	-2		0,4	0,7	0,8	0,9
l2		0,9	0,8	0,6	0,4		-0,8	-2,4	-5,1	-7,3	+∞

Определим масштабный коэффициент построения графика коэффициентов удельного скольжения:

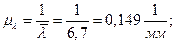
где 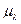─ масштабный коэффициент построения графика коэффициентов скольжения, 1/мм;

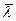─ принятое значение на графике, мм;

Данные заносим в таблицу 4.3:

Таблица 4.3 ─ Значения коэффициентов скольжения на графике, мм
	N1	a				W			b		N2
	-∞	-45	-44,3	-20,8	-13,4		2,7	4,7	5,4		6,7
	6,7		5,4		2,7		-5,4	-16	-34,2	-50	-∞

Строим график коэффициентов скольжения.

Дата добавления: 2015-09-01