Методы минимизации

Численные методы отыскания минимумов функций многих переменных. Пусть задана ограниченная снизу дважды непрерывно дифференцируемая по своим аргументам функция

для к-рой известно, что при нек-ром векторе ( - знак транспонирования) она принимает наименьшее значение. Требуется построить последовательность векторов такую, что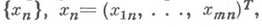

Существует много методов, позволяющих получить указанную последовательность векторов. Однако общим недостатком большинства алгоритмов является резкое ухудшение их свойств в случаях, когда поверхности уровня минимизируемой функции имеют структуру, сильно отличающуюся от сферической. В этом случае нек-рую область , в к-рой норма вектора-градиента существенно меньше, чем в остальной части пространства, наз. дном оврага, а саму функцию - овражной функцией. Если размерность пространства аргументов минимизируемой функции больше двух, то структура поверхностей уровня овражных функций может оказаться весьма сложной. Появляются (т-к)-мерные овраги, где число кизменяется от 1 до т-1. В трехмерном пространстве, напр., возможны одномерные и двумерные овраги.

Функции овражного типа локально характеризуются плохой обусловленностью матриц двух производных (матриц Гессе)

что приводит к сильному изменению функции вдоль направлений, совпадающих с собственными векторами матрицы Гессе для больших собственных чисел, и к слабому изменению вдоль других направлений, отвечающих малым собственным значениям матрицы Гессе. Большинство известных методов оптимизации позволяет достаточно быстро попадать на дно оврага, приводя иногда к существенному уменьшению значения функции J(х)по сравнению с его значением в начальной точке (спуск на дно оврага). Однако далее процесс резко замедляется и практически останавливается в нек-рой точке из Q, к-рая может быть расположена очень далеко от истинной точки минимума.

Дважды непрерывно дифференцируемая по своим аргументам функция J(х)наз. овражной функцией (см. [1]), если существует нек-рая область , где собственные значения матрицы Гессе 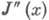, упорядоченные в любой точке по убыванию модулей, удовлетворяют неравенствам

Степень овражности характеризуется числом

Если собственные значения 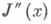в области Gудовлетворяют неравенствам

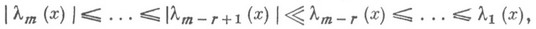
то число r наз. размерностью оврага функции при (см. [1]).

Системы дифференциальных уравнений, описывающие траекторию спуска овражной функции ,

являются жесткими дифференциальными системами. В частности, когда функция J(х)сильно выпуклая и матрица Гессе положительно определена (все ее собственные значения строго больше нуля), неравенства (1) совпадают с известным требованием плохой обусловленности матрицы Гессе

В этом случае спектральное число обусловленности совпадает со степенью овражности.

Метод покоординатного спуска (см. [2])

несмотря на простоту и универсальность, в овражной ситуации эффективен лишь в редких случаях ориентации оврагов вдоль координатных осей.

Предложена (см. [2]) модернизация метода (4), состоящая в использовании процедуры вращения осей координат так, чтобы одна из осей была направлена вдоль после чего начинается поиск на (k+1)-м шаге. Такой подход приводит к тому, что одна из осей имеет тенденцию выстраиваться вдоль образующей дна оврага, позволяя в ряде случаев весьма успешно проводить минимизацию функций с одномерными оврагами. В случае многомерных оврагов метод непригоден.

Схема метода наискорейшего спуска задается разностным уравнением

где выбирается из условия

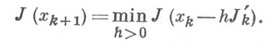
Для сильно выпуклой овражной функции, в частности квадратичной

последовательность построенная алгоритмом (5), сходится к точке минимума функции по закону геометрия, прогрессии (см. [3])

где С=const,

Так как для овражной функции 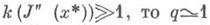и сходимость практически отсутствует.

Аналогичная картина наблюдается и для простой градиентной схемы (см. [4])

Ускорение ее сходимости основано на использовании результатов предыдущих итераций для уточнения дна оврага. Может быть использован (см. [4] [5]) градиентный метод (7) с вычислением на каждой итерации отношения Когда оно устанавливается около нек-рого постоянного значения , делается большой ускоряющий шаг согласно выражению

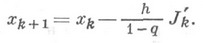
Далее из точки x_k+1 продолжается спуск градиентным методом до следующего ускоряющего шага.

Различные версии метода параллельных касательных (см. [4] - [6]) основаны на выполнении ускоряющего шага вдоль направления задаваемого точками в градиентном методе. В методе "тяжелого шарика" (см. [4]) очередное приближениеимеет вид

Вметоде оврагов (см. [7]) предлагается провести локальные спуски градиентным методом (7) из двух случайно выбранных исходных точек, а затем выполнить ускоряющий шаг по направлению, задаваемому двумя полученными на дне оврага точками.

Все эти методы немногим сложнее градиентного метода (7) и построены на его основе. Ускорение сходимости получается для одномерных оврагов. В более общих случаях многомерных оврагов, где сходимость этих схем резко замедляется, приходится обращаться к более мощным методам квадратичной аппроксимации, в основе к-рых лежит метод Ньютона

Точка минимума функции (6) удовлетворяет системе линейных уравнений

и при условии абсолютной точности всех вычислений для квадратичной функции метод Ньютона независимо от степени овражности (2) и размерности оврагов приводит к минимуму за один шаг. На самом деле, при больших числах обусловленности k(D)при ограниченной разрядности вычислений задача получения решения (9) может быть некорректной, и небольшие деформации элементов матрицы Dи вектора могут приводить к большим вариациям

При умеренных степенях овражности в выпуклой ситуации метод Ньютона часто оказывается более предпочтительным по скорости сходимости, чем другие, напр, градиентные, методы.

Большой класс квадратичных (квазиньютоновских) методов основан на использовании сопряженных направлений (см. [2], [3], [8]). Эти алгоритмы для случая минимизации выпуклой функции оказываются весьма эффективными, ибо, имея квадратичное окончание, они не требуют вычисления матрицы двух производных.

Иногда (см. [8]) итерации строятся по схеме

где Е- единичная матрица. Скаляр подбирается так, чтобы матрица была положительно определенной и чтобы

Существует ряд аналогичных подходов (см. [8]), основанных на получении строго положительно определенных аппроксимаций матрицы Гессе. При минимизации овражных функций такие алгоритмы оказываются малоэффективными из-за трудностей в подборе параметров и т. д. Выбор этих параметров основан на информации о величине наименьших по модулю собственных значений матрицы Гессе, а при реальных вычислениях и большой степени овражности эта информация сильно искажена.

Более целесообразно обобщение метода Ньютона на случай минимизации овражных функций проводится на базе непрерывного принципа оптимизации. Функции J(х)ставится в соответствие дифференциальная система (3), интегрируемая системным методом (см. Жесткая дифференциальная система). Алгоритм минимизации принимает вид

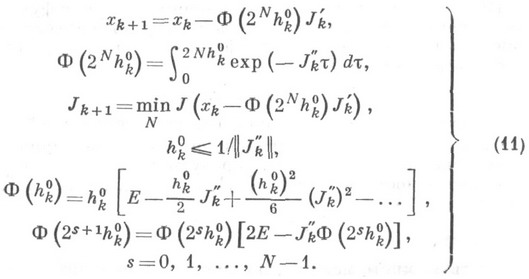
Предложен [1] алгоритм минимизации овражной функции, основанный на использовании свойств жестких систем. Пусть функция в окрестности аппроксимируется квадратичной функцией (6). Матрица Dи вектор вычисляются, напр., с помощью конечно-разностной аппроксимации. Из представления элементов матрицы

где 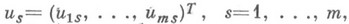-ортонормированный базис собственных векторов D, следует, что неточное измерение этих элементов искажает информацию о малых собственных значениях плохо обусловленной матрицы, а следовательно, приводит к некорректности задачи минимизации функции (6).

Вместе с тем система дифференциальных уравнений спуска для овражной функции (6)

имеет решение, в к-ром в силу условия (1) слагаемые с сомножителями оказывают влияние лишь на малом начальном отрезке длиной

Другими словами, компоненты вектора х(t)удовлетворяют равенству

быстро переходящему в стационарную связь

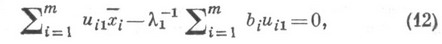
где - компоненты вектора, удовлетворяющие равенству (12). Это свойство используется в алгоритме. Выражая j-ю компоненту вектора , к-рой соответствует максимальная компонента вектора , через остальные компоненты, вместо функции , получают новую функцию с аргументом размерности :

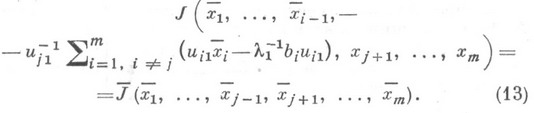
По функции (13) с помощью конечноразностной аппроксимации находится новая матрица порядка (т-1) и вектор Здесь важно не только и не столько понижение размерности пространства поиска, сколько уменьшение степени овражности, т. к. при минимизации новой функции в подпространстве, ортогональном вектору u₁, большое собственное значение уже не оказывает влияния на вычислительный процесс. Самым существенным моментом здесь является требование получения 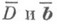по функции (13), а не по матрице Dи вектору . Коэффициенты связи (12) находят степенным методом, как коэффициенты любого уравнения системы

Если степень овражности не понижается или понижается незначительно, то процесс исключения координат вектора хпродолжается рекурсивно до необходимого ее уменьшения.

Операции с выпуклыми функциями

Теорема.

Пусть функции f1 и f2

замкнуты и выпуклы, и пусть β ≥0. Тогда все нижеследующие функции также замкнуты и выпуклы:

1) f (x)=β f1(x), dom f =dom f1;

2) f (x)= f1(x)+ f2(x), dom f =(dom f1) ∩ (dom f2);

3) f (x)=max{f1(x), f2(x)}, dom f =(dom f1) ∩ (dom f2).

Доказательство.

1. Для первой функции утверждение очевидно:

f (αx1+(1−α)x2)≥β(αf1(x1)+(1−α) f1(x2)).

2. Для всех x1, x2 ∈ (dom f1) ∩ (dom f2) и α ∈ [0, 1] имеем

f1(αx1+(1−α)x2)+ f2(αx1+(1−α)x2)≤αf1(x1)+(1−α) f1(x2)+αf2(x1)+(1−α)f2(x2)=

=α(f1(x1)+ f2(x1))+(1−α)(f1(x2)+ f2(x2)).

Таким образом, функция f (x) выпукла. Докажем ее замкнутость.

Рассмотрим последовательность {(xk, tk)}⊂epi(f):

tk ≥ f1(xk)+ f2(xk), limk→∞xk = x¯ ∈domf, limk→∞tk =¯t.

Поскольку f1 и f2 –– замкнутые функции, справедливо неравенство

inflimk→∞f1(xk)≥ f1(x¯), inflimk→∞f2(xk)≥ f2(x¯).

Поэтому¯t= limk→∞tk ≥inflimk→∞f1(xk)+inflimk→∞f2(xk)≥ f (x¯).

Значит 1, (¯x,¯t) ∈epi f.

3. Надграфик функции f (x) запишется в виде

epif ={(x, t) | t≥ f1(x)t≥ f2(x)x∈ (domf1) ∩ (domf2) }≡epif1 ∩ epif2.

Значит, epi f –– замкнутое и выпуклое множество как пересечение

двух замкнутых и выпуклых множеств.

Заключение.

В данной курсовой работе мы рассмотрели некоторые простые и улучшенные методы минимизации, метод парабол. Так же мы проанализировали эти методы, и выяснили, какие из них более эффективны и в каких случаях.

Список используемых источников

1. Евтушенко, Ю. Г. Методы решения экстремальных задач и их применение в системах оптимизации. М.: Наука, 1982. 432.

2Полак, Э. Численные методы оптимизации. М: Мир, 1974. 376 с..

3. Гилл, Ф. Практическая оптимизация/ Ф. Гилл, У., Мюррей, М. Райт. М.: Мир, 1985. 509с.

4. Зангвилл, У. И. Нелинейное программирование. Единый подход. М.: Сов.радио, 1973.

Дата добавления: 2015-09-01