Определение чисел зубьев колес

Числа зубьев подбирают после выбора передаточною от­ношения и числа сателлитов в зависимости от кинемати­ческой схемы передачи и конструкции (редуктор или мотор-редуктор).

Подбор чисел зубьев колес для схем 1, 2 и соответствую­щих им ступеней сложных передач, выполненных по схеме 5 (см. табл. 5.1.). Принимают число зубьев солнечного колеса z ₁ ³ 13 (во избежание подрезания ножек зубьев); числа зубьев сателлитов z ₂ определяют по формуле

(5.11)

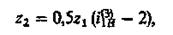
округляя до ближайшего целого числа. Число зубьев корон­чатого колеса z ₃ определяют по формуле (5.2).

По формулам табл. 5.1 уточняют передаточное отношение и сравнивают его с заданным. Допускается отклонение не более чем на 4% для одноступенчатых редукторов, 5% —для двух­ступенчатых. Далее проверяют выполнение условий вхождения зубьев в зацепление и соседства.

Пример 1. Подобрать числа зубьев колес планетарного ре­дуктора по рис. 5.1 с передаточным соотношением i ⁽³⁾_{1 H} = 5,6 и числом сателлитов n _с = 3.

1.Выбираем число зубьев солнечного колеса z ₁ = 15.

2. Определяем число зубьев сателлитов по формуле (5.11)

Проверяем условие вхождения зубьев в зацепления по фор­муле (5.10)

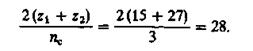
Условие выполнено.

4. Проверяем выполнение условия соседства по формуле (5.9)

Условие выполнено.

5. Число зубьев корончатого колеса по формуле (5.2)

6. Уточняем передаточное отношение по формуле табл. 5.1

что соответствует заданному.

Порядок подбора чисел зубьев передачи по схеме 1, выпол­ненной как мотор-редуктор специального назначения (его пара­метры не регламентированы ГОСТ) имеет свои особенности, поясненные ниже численным примером.

Пример 2. Подобрать числа зубьев колес мотор-редукгора специального назначения по схеме 1 (см. табл. 5.1) с переда­точным отношением i ⁽³⁾_{1 H} = 6,3 и числом сателлитов п_с = 3. Присоединяемый электродвигатель 4А112М2УЗ, наружный диа­метр фланца D = 300 мм.

1. Определяем делительный диаметр d ₃, корончатого колеса
d ₃ » D ¾ (30¸40) = 300 ¾ (30¸40) = 270¸260 мм.

Ряд делительных диаметров (в мм) по ГОСТ 25022-81 следующий: 100; 125; 160; 200; 250; 315; 400; 500; 630; 800; 1000. Принимаем ближайшее значение d ₃ = 250 мм. Соответст­венно т = 2 мм.

2. Определяем число зубьев корончатого колеса

3. Число зубьев солнечного колеса определяем на основании формулы

(см. табл. 5.1.), откуда

Принимаем z ₁ = 24.

4. Число зубьев сателлита — по формуле (5.2)

Принимаем z ₂ = 51, тогда z₃ = z ₁ + 2z₂ = 24 + 2 × 51 = 126.

5. Проверка условия вхождения зубьев в зацепление:

6. Проверка условия соседства

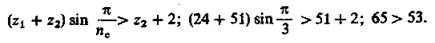
7. Уточняем передаточное отношение

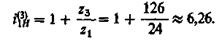
8. Отклонение его от заданного

что допустимо (D _{i max} = 4%).

Окончательное значение чисел зубьев: z ₁ = 24; z ₂ = 51; z ₃ = 126; m = 2 мм; d ₃ = mz ₃ = 2 × 126 = 252 мм.

ГОСТ 250022-81 допускает отклонение значения делитель­ного диаметра корончатого колеса 3 от номинального в пре­делах допускаемых отклонений передаточного отношения.

Для предварительного выбора чисел зубьев колес плане­тарных передач по схемам 1 и 2 (см. табл. 5.1) удобно пользоваться табл. 5.2.

5.2. Таблица передаточных отношений и чисел зубьев колес для схемы рис. 5.1

z 1	z 2	z 3
	16-20 15-23 16-24 15-27 15-27 16-28 16-30 15-31 16-34 15-35 16-38 15-39 16-42 17-45 18-46 19-40 18-50	17-15 20-16 22-18 24-18 25-19 26-20 27-20 30-22 32-23 35-25 37-26 40-28 42-29 44-30 46-32 48-33 51-35	4,125-3,500 4,670-3,391 4,750-3,500 5,200-3,333 5,333-3,407 5,250-3,429 5,375-3,333 6,000-3,419 6,000-3,353 6,667-3,429 6,625-3,368 7,333-3,346 7,250-3,381 7,176-3.333 7,111-3,391 7,053-3,347 7,666-3,400	1,320-1,400 1,273-1,418 1,267-1,400 1,238-1,429 1,231-1,415 1,235-1,412 1,229-1,429 1,200-1,413 1,200-1,425 1,176-1,412 1,178-1,422 1.158-1,411 1.160-1,420 1,162-1,428 1,163-1,418 1,165-1,426 1,150-1,418
Принятые обозначения: z 1 — число зубьев солнечного колеса (изменяется через два зуба); z 2 — число зубьев сателлита (изменяется через один зуб): z 3 — число зубьев корончатого колеса: Н —водило.

Подбор чисел зубьев колес передач по схеме 3 (см. табл. 5.1). Передача по схеме 3 — однопоточная, поэтому под­бор чисел зубьев колес обусловливается только соосностью двух пар колес 1-2 и 2'-3, а также выполнением задан­ного передаточного отношения. Если модули зацеплений обеих пар колес равны и зубья нарезаны без смещения зуборез­ного инструмента, то условие соосности можно выразить через числа зубьев

(5.12)

Зависимость чисел зубьев от передаточного отношения

(5.13)

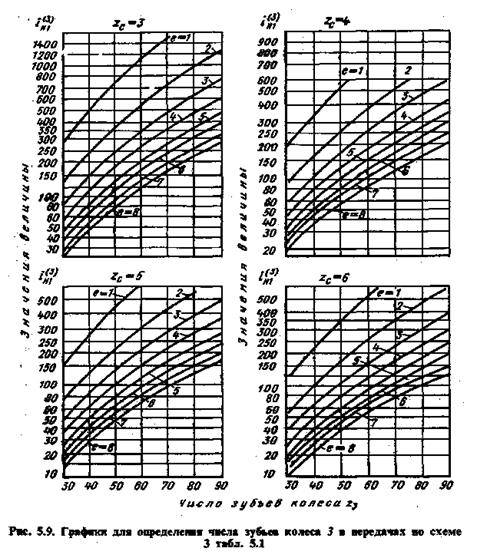
Решение этой системы уравнений дано на графиках (рис. 5.9), где по заданному передаточному отношению, за­даваясь разностями чисел зубьев z _c = z₁ — z₂ = z ₃ — z _2¢ и е = z ₃ — z ₁ = z _2¢ — z ₂, можно определить значение z ₃.

По графику (рис. 5.10) можно определить минимальные значения z _c, при которых не будет интерференции головок зубьев шестерни и колеса; если значение z _c меньше указан­ного на графике, то для устранения интерференции колеса надо нарезать со смещением зуборезного инструмента или (когда z _c ³ 3) применять зуборезный инструмент с углом профиля 30^о и коэффициентом высоты головки зуба h * _a = 0,8.

1. Принимаем z _c = z₁ — z₂ = z ₃ — z _2¢ и е = z ₃ — z ₁ = z _2¢ — z ₂ = 5.

2. По графику (рис. 5.9) находим z ₃ = 84.

3. Определяем

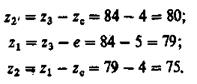
4. Фактическое передаточное отношение

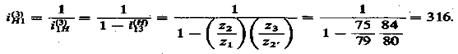
5. Отклонение фактического передаточного отношения от заданного

РАСЧЕТ ЗУБЬЕВ ПЛАНЕТАРНЫХ ПЕРЕДАЧ

Дата добавления: 2015-09-05