НА ПРОЧНОСТЬ

В планетарных передачах, где сателлит входит в зацепле­ния с двумя центральными колесами (солнечным и корончатым) и механические характеристики материала колес примерно одинаковы, рассчитывают на прочность только внешнее за­цепление (солнечное колесо — сателлит). При определении числа циклов нагружения зубьев надо учитывать только относитель­ную частоту вращения колес, т. е. при остановленном водиле. Для передач с вращающимся центральным колесом 1 и не­подвижным п относительные частоты вращения колес опреде­ляют по формулам

(5.14)

В табл. 5.1 для каждой передачи приведена формула для определения относительной частоты вращения сателлита, ис­пользуемая при расчете долговечности ею подшипников.

Порядок расчета зубьев планетарных передач на прочносгь зависит от задания на проектирование. При проектировании планетарной передачи как отдельной сборочной единицы расчет следует начинать с определения межосевого расстояния го условия контактной прочности. При проектировании мотор-редуктора диаметр передачи определяется диаметром корпуса присоединяемого электродвигателя, поэтому расчет удобно начинать с определения ширины колес из условий контактной и изгибной прочности. Окончательная ширина колес опреде­лится после подбора подшипников сателлитов.

Формулы для расчета на прочность зубьев планетарных передач приведены в табл. 5.3.

Величины сил и вращающих моментов, действующих на звенья планетарных передач, не зависят от числа степеней свободы. В передачах с одной степенью свободы вращающий момент, действующий на неподвижное центральное колесо, уравновешивается реакциями мест закрепления.

В многопоточных передачах (рис. 5.11) в установившемся режиме работы силы в зацеплениях, действующие на цент­ральные колеса и водило, уравновешивают друг друга, и поэтому валы нагружены только вращающим моментом. Силы зацеплений, действующие на сателлиты, приложены на диамет­рально противоположных сторонах, поэтому их радиальные составляющие уравновешивают друг друга, а окружные складываются, так как

Рис. 5.11. Взаимное уравновешивание сил, действующих в многопоточных передачах

Формулы для расчета на прочность зубьев планетарных передач

Расчетная зависимость	Единицы измерения	№ формулы
Прочность рабочих поверхностей Проектировочный расчет Межосевое расстояние   Ширина колес Проверочный расчет Расчетное контактное напряжение     Изгибная прочность   Проектировочный расчет Ширина колес Модуль     Расчетное напряжение изгиба	мм   мм   МПа   МПа     мм     мм   МПа   МПа	(5.15)   (5.16)   (5.17)   (5.18)     (5.19)     (5.20)   (5.21)   (5.22)
П р и м е ч а н и я: 1. Расшифровка обозначение параметров, их величины и размерности, кроме указанных ниже, см. в §3.2. и 3.3. 2. В формулах (5.16)-(5.21) знак плюс для наружного зацепления, знак минус для внутреннего. 3. u = z2 / z1 – отношение чисел зубьев большего колеса рассчитываемой пары к меньшему (u ³ 1). 4. Т 2 – вращающий момент, действующий на большее колесо рассчитываемой пары. 5. Приведенное число сателлитов (с учетом неравномерного распределения нагрузки между ними) n¢c = nc – 0,7

Рис. 5.12. Силовой расчет перадчи по схемам 1 и 2 таюл. 5.1. и рис. 5.1 – 5.4:

они параллельны и направлены в одну сторону; суммарная нагрузка действует на подшипники и оси сателлитов.

При проведении силового расчета удобно пользоваться ме­тодом, представленным на рис. 5.12 и 5.13, где последова­тельно рассматривается равновесие каждого звена передачи. Начинать расчет следует со звена, на котором задан вращаю­щий момент, по его значению и размерам колес находят уравновешивающую силу; затем на основании равенства дей­ствующей и противодействующей сил находят силу, действую­щую на звено, входящее в кинематическую пару. Далее рас­сматривают равновесие второго звена, находят уравновеши­вающую силу или момент и т. д., пока не будет рассмот­рено равновесие всех звеньев передачи.

Все силы обозначены буквой F с двумя нижними цифровыми индексами: первый указывает номер звена, со стороны которого действует сила, второй -

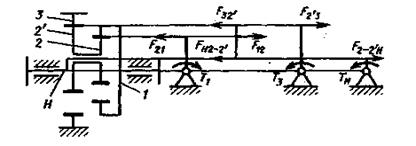
Рис. 5.13. Силовой расчет передачи по схеме 3 табл. 5.1:

— звено, на которое действует сила. Например, F₁₂ — окружная сила, с которой колесо 1 действует на колесо 2.

Проверкой правильности силового расчета служит уравне­ние равновесия внешних вращающих моментов, приложенных к передаче (в том числе и опорный момент).

Пример. Для передач по рис. 5.1 — 5.4 определить окружные силы в зацеплениях, внешние вращающие моменты, действую­щие на центральные звенья, и силу, действующую на под­шипник сателлита и его ось. Задан момент Т _нполезного сопротивления, приложенный к водилу, размеры колес и число сателлитов п _с.

1. Рассматриваем равновесие водила и находим силу F_2н (см. рис. 5.12)

2. Рассматриваем равновесие сателлита, который входит в кинематические пары с водилом и центральными колесами 1 и 3, и находим силы F₁₂ и F₃₂

Условие равенства моментов сил относительно оси сател­лита

3. Рассматриваем равновесие центрального колеса 3 и нахо­дим вращающий момент

Для передачи по рис. 5.2 момент Т ₃ — ведущий, для передачи по рис. 5.3 — полезного сопротивления, для передачи по рис. 5.1 — опорный.

4. Рассматриваем равновесие центрального колеса 1 и на­ходим момент

Вращающий момент Т ₁, в рассматриваемом примере для передачи по рис. 5.1, 5.2, 5.3 - движущий (без учета потерь).

С учетом потерь движущий момент Т¢ ₁ = T₁ / h, где h - КПД передачи (см. табл. 5.1).

На рис. 5.13 приведен пример силового расчета передачи по схеме 3 для случая, когда задан вращающий момент (момент полезного сопротивления) на ведомом колесе 1.

Рис. 5.14. Планетарный редуктор по схеме 1 табл. 5.1 с плавающим корончатым колесом

Рис. 5.15. Лебедка с планетарным редуктором по схеме 1 табл. 5.1.

КОНСТРУКЦИИ ПЛАНЕТАРНЫХ ПЕРЕДАЧ

Конструкции планетарных передач зависят от выбранной кинематической схемы, величины передаваемого вращающего момента и срока службы. Для получения меньших габаритов силовые передачи выполняют многопоточными (обычно трехпоточными). Следует назначать нечетное число сателлитов для лучшего уравновешивания сил в зацеплениях.

Конструкции центральных колес. Для равномерного распре­деления нагрузки между сателлитами силовых многопоточных передач одно или оба центральных колеса делают самоуста­навливающимися (плавающими) (рис. 5.14). В передачах, имею­щих большие габариты, плавающим делают оба центральных колеса: самоустановка достигается применением зубчатых муфт, соединяющих солнечные колеса с ведущим валом или водилом предыдущей ступени, а корончатые колеса с корпусом или замыкающей передачей.

В конструкциях на рис. 5.15—5.17 самоустановка достигает­ся применением гибких элементов. На рис. 5.15 солнечное колесо расположено консолыго па длинном гибком валу. На рис. 5.16 в конструкцию корончатого колеса включена гибкая оболочка. На рис. 5.17 сателлит установлен на гибкой оси.

Для равномерного распределения нагрузки между сателли­тами возможен и другой путь — жесткая установка всех деталей передачи при условии высокой точности их изготовления и монтажа (рис. 5.18). Жесткие корончатые колеса могут быть нарезаны непосредственно на корпусе, запрессованы в корпус или установлены в разъеме фланцев (рис. 5.19).

Конструкции сателлитов. Сателлиты обычно делают с внут­ренней расточкой под подшипники качения. Для самоустановки применяют сферические подшипники. Максимальный диаметр наружного кольца подшипника

D _max = т (z - 7 ), (5.23)

где т — модуль колеса передачи; z — число зубьев сателлита.

Устанавливать сателлит на двух или трех подшипниках часто приходится для получения заданного срока службы пере­дачи (рис. 5.20). При малых диаметрах сателлитов подшип­ники устанавливают в щеках водила (рис. 5.20, д)или приме­няют подшипники без колец. При невозможности обеспечить заданную долговечность подшипниками качения сателлиты устанавливают на подшипниках скольжения.

Сателлиты с двумя венцами обычно делают сборными (рис. 5.21), что позволяет уменьшить массу заготовок и сокра­тить время механической обработки. Сдвоенные сателлиты, устанавливаемые в одну передачу, должны иметь одинаковое относительное расположение зубьев венцов. Для этого их собирают в специальных приспособлениях или применяют конструкции, позволяющие устанавливать взаимное расположе­ние венцов при сборке (рис. 5.22). Делать сдвоенные сателлиты одной деталью следует только в тех случаях, когда их диа­метры мало отличаются друг от друга.

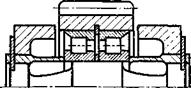
Рис. 5.16. Конструкция корончатого Рис. 5.17. Конструкция сателлита

Дата добавления: 2015-09-05