Математика в стародавньому Китаї

Китайська версія пифагоровой трійки:
3 4 5

Перші дійшли до нас китайські писемні пам'ятки відносяться до епохи Шан (XVIII-XII ст. до н. е..). І вже на гадальних кістках XIV ст. до н. е.., знайдених в Хенань, збереглися позначення цифр. Але справжній розквіт науки почався після того, як в XII в. до н. е.. Китай був завойований кочівниками Чжоу. У ці роки виникають і досягають дивовижних висот китайська математика і астрономія. З'явилися перші точні календарі та підручники математики. "Винищення книг" імператором Цинь Ши Хуаном (Ши Хуанді) не дозволило раннім книгам дійти до нас, однак вони, швидше за все, лягли в основу подальших праць.

З царювання династії Хань (II ст. до н. е.. - I ст. н. е..) древні знання стали відновлювати і розвивати. У II ст. до н. е.. опубліковані найбільш древні з дійшли до нас творів - математико-астрономічний "Трактат про вимірювальному жердині" і фундаментальна праця " Математика в дев'яти книгах "("九章算术").

Цифри позначалися спеціальними ієрогліфами, які з'явилися в II тисячолітті до н. е.., і знамено їх остаточно встановилося до III в. до н. е.. Ці ієрогліфи застосовуються і в даний час. Китайський спосіб запису чисел спочатку був мультиплікативним. Наприклад, запис числа 1946, використовуючи замість ієрогліфів римські цифри, можна умовно уявити як 1М9С4Х6. Однак на практиці розрахунки виконувалися на лічильної дошці суаньпань, де запис чисел була іншою - позиційної, як в Індії, і, на відміну від вавилонян, десяткової.

Японські рахунки

Китайська лічильна дошка за своєю конструкцією аналогічна російським рахунками. Нуль спочатку позначався порожнім місцем, спеціальний ієрогліф з'явився близько XII століття н. е.. Для запам'ятовування таблиці множення існувала спеціальна пісня, яку учні заучували напам'ять.

Математика в дев'яти книгах (початок)

Престиж математики в Китаї був високий. Кожен чиновник, щоб отримати призначення на посаду, здавав, крім інших, і іспит з математики, де зобов'язаний був показати вміння вирішувати завдання з класичних збірок. Найбільш змістовне математичний твір стародавнього Китаю - " Математика в дев'яти книгах "(Цзю чжан суань шу). Це слабо узгоджена компіляція старіших праць різних авторів. Книга була остаточно відредагована фінансовим чиновником Чжан Цаном (помер в 150 р. до н. е..) і призначена для землемірів, інженерів, чиновників і торговців. У ній зібрати 246 завдань, викладених у традиційному східному дусі, тобто рецептурно: формулюється завдання, повідомляється готову відповідь і (дуже коротко і не завжди) вказується спосіб вирішення.

У IV ст. н. е.. китайці уточнюють число π - Спочатку як 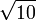, Потім як 142/45 = 3,155..., а пізніше (V століття) як 3,1415926, причому відкривають для нього відоме раціональне наближення: 355/113.

У цей час китайцям вже було відомо багато чого, в тому числі:

• вся базова арифметика (включаючи перебування найбільшого загального дільника і найменшого спільного кратного);
• дії з дробами і пропорції;
• дії з негативними числами (фу), які трактували як борги;
• рішення квадратних рівнянь.

Був навіть розроблений метод фан-Чен (方程) для вирішення систем довільного числа лінійних рівнянь - аналог класичного європейського методу Гауса. Чисельно вирішувалися рівняння будь-якого ступеня - способом тянь-юань (天元术), що нагадує метод Руффини-Горнера для знаходження коренів многочлена.

У галузі геометрії їм були відомі точні формули для визначення площі та обсягу основних фігур і тіл, теорема Піфагора і алгоритм підбору піфагорових трійок.

В III столітті н. е.. під тиском традиційної десяткової системи заходів з'являються і десяткові дроби. Виходить "Математичний трактат" Сунь-Цзи. У ньому, крім іншого, вперше з'являється завдання, якій пізніше в Європі займалися найбільші математики, від Фібоначчі до Ейлера і Гаусса: знайти число, яке при діленні на 3, 5 і 7 дає відповідно залишки 2, 3 і 2. Завдання такого типу нерідкі в теорії календаря.

Інші теми дослідження китайських математиків: алгоритми інтерполяції, підсумовування рядів, тріангуляція.

Дата добавления: 2015-09-05