Задача управления запасами состоит в отыскании такого запаса s, при котором математическое ожидание суммарных затрат (28) или (29) принимает минимальное значение.

Доказано математически, что при дискретном случайном спросе r выражение (28) минимально при запасе s₀, удовлетворяющем неравенствам:

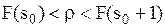(30)

а при непрерывном случайном спросе r выражение (29) минимально при значении s₀, определяемом из уравнения

(31)

где

(32)

есть функция распределения спроса r, F(s₀) и F(s₀+1) – её значения; r – плотность убытков из-за неудовлетворенного спроса, определяемая по (24).

Оптимальный запас при непрерывном спросе по данному значению r может быть найден и графически (рис. 5).

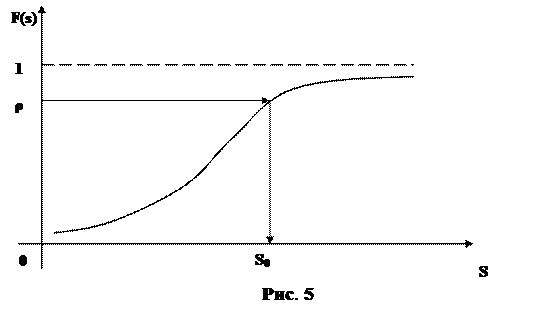Задача 5. П редприятие закупает агрегат с запасными блоками к нему. Стоимость одного блока равна 5 ден. ед. В случае выхода агрегата из строя из-за поломки блока, отсутствующего в запасе, простой агрегата и срочный заказ нового блока к нему обойдётся в 100 ден. ед. Опытное распределение агрегатов по числу блоков, потребовавших замену таково: в прошлом году поступило 100 агрегатов. У девяноста из них вообще замена блоков не потребовалась, у пяти агрегатов из 100 поступивших потребовалась в течение 1 года замена 1 блока, у двух агрегатов замена 2 блоков, у одного агрегата заменили в течение года 3 блока, у одного агрегата – 4 блока, и ещё у одного агрегата заменили в процессе работы 5 блоков. Больше чем 5 блоков не заменяли ни у одного из поступивших агрегатов. Представим опытное распределение агрегатов по числу заменённых блоков в табл. 1.

Таблица 1

Число заменённых блоков r
Статистическая вероятность (доля) агрегатов р(r), которым потребовалась замена r блоков		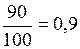	0,02	0,01	0,01	0,01	0,00

Необходимо определить оптимальное число запасных блоков, которое следует приобрести вместе с каждым агрегатом.

Решение. По условию задачи 5 с₂ = 5 ден. ед., с₃ = 100 ден. ед. Вычислим плотность убытков из-за нехватки запасных блоков по формуле (24) r=100/(5+100)=0,952.

Учитывая (32), найдём значения функции распределения спроса F(s) и запишем найденные значения в табл. 2. В таблице 2 пусть запас блоков s составит 0 блоков, тогда по выражению (32) вероятность того, что спрос r меньше запаса блоков s=0, будет p(r<s)=F(0)=0 (т.е. вероятность равна нулю). Пусть запас блоков s=1, тогда вероятность того, что спрос r меньше запаса блоков s=1, равна вероятности 0,9, т.е. вероятности того, что спрос примет значение r=0. Пусть запас блоков s=2, тогда вероятность того, что спрос r будет меньше запаса блоков s=2 равен вероятности 0,95, при которой спрос принимает значение либо r=0, либо r=1, т.е. p(r<s) =F(s)=0,9+0,05=0,95 и т.д.

Таблица 2

S	r	p(r<s)=F(s)
		0,9 (из табл.1)
		из табл.1 (0,9+0,05=0,95)
		0,9+0,05+0,02=0,97
		0,98
		0,99
		1,0
> 6	> 6	1,0

Очевидно (см. табл. 2), что оптимальный запас составит s₀=2 блока, т.к. он удовлетворяет неравенству (30): F(2)=0,95<0,952<F(3)=0,97.

Задача 6. Решить задачу 5 при условии непрерывного случайного спроса r, распределённого по показательному закону с функцией распределения при l=0,98.

Решение. Оптимальное число запасных блоков s₀ найдём из уравнения (31) (): откуда и .

При l = 0,98 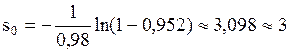(блока).

[1] С помощью достаточного условия экстремума можно убедиться в том, что действительно при n = n₀, s = s₀ функция С(n,s) достигает минимума.

Дата добавления: 2015-09-05