Читайте также:
|
Векторное параметрическое уравнение прямой в пространстве:
где 
— радиус-вектор некоторой фиксированной точки M 0, лежащей на прямой, 
— ненулевой вектор, коллинеарный этой прямой,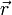 
— радиус-вектор произвольной точки прямой.
Параметрическое уравнение прямой в пространстве:
где 
— координаты некоторой фиксированной точки M 0, лежащей на прямой; 
— координаты вектора, коллинеарного этой прямой.
Каноническое уравнение прямой в пространстве:
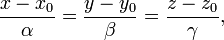
где — координаты некоторой фиксированной точки M 0, лежащей на прямой; — координаты вектора, коллинеарного этой прямой.
Общее векторное уравнение прямой в пространстве:
Поскольку прямая является пересечением двух различных непараллельных плоскостей, заданных соответственно общими уравнениями:
и 
то уравнение прямой можно задать системой этих уравнений:
Дата добавления: 2015-09-05; просмотров: 46 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Параметрические уравнения прямой | | | Взаимное расположение точек и прямых на плоскости |