Задание 1.5

Для системы вода-пробка записать передаточную функцию (вход - задание положение, выход - глубина погружения). Определить переходную и частотные характеристики.

Передаточная функция для системы вода-пробка:

Без учета силы сопротивления:

C учетом силы сопротивления:

Переходная характеристика без учета силы сопротивления: АФХ

ЛАЧХ

ЛФЧХ

Переходная характеристика с учетом силы сопротивления:

АФХ

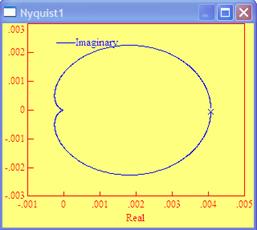
ЛАЧХ

ЛФЧХ

Контрольные вопросы:

1) Передаточная функция без учета сопротивления: ξ = 0,

Консервативное звено, в зависимости от его изменения, изменяется амплитуда переходной характеристики.

ω – сопрягающая частота – примерно равна 20 Гц;

Фаза достигает значения -180 градусов, коэффициент k меньше единицы;

АФХ охватывает точку (-1; j0), крайняя точка справа на АФХ соответствует нулевой частоте, крайняя левая – частоте, стремящейся к бесконечности. Положительным частотам соответствует нижняя траектория

2) Передаточная функция с учетом сопротивления: колебательное звено.

в зависимости от его изменения, изменяется амплитуда переходной характеристики.

ω – сопрягающая частота – примерно равна 20 Гц;

Фаза достигает значения -180 градусов, коэффициент k меньше единицы;

АФХ не охватывает точку (-1; j0), крайняя точка справа на АФХ соответствует нулевой частоте, крайняя левая – частоте, стремящейся к бесконечности. Положительным частотам соответствует нижняя траектория

Задание 1.6

Определить: а) коэффициент усиления К и постоянную времени Т апериодического звена первого порядка. 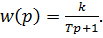б) постоянную интегрирования T интегрирующего звена

по графику переходных процессов:

а) апериодическое звено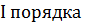

б) интегрирующее звено

Выполним задание под (а)

k_утс = 11,3 t_уст = 35,0

Для аппериодичского звена переходная функция:

При, т. е.

Для определения постоянной времени воспользуемся условием попадания в 5% зону:

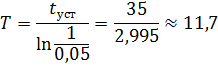
Выполним задание под (б)

Переходная функция интегрирующего звена в нашем случае(оно же уравнение прямой в нашем случае) равна

Возьмём наши данные из таблицы

Из переходной функции выразим k

Теперь возьмём обратное преобразование лапласа и получим переходную функцию интегрирующего звена:

Приравняем

По свойству пропорции найдём T:

Задание №7.

Аналитически определить время окончания переходного процесса для передаточной функции апериодического звена

Тоже самое что и (в 6 задании) под буквой (а) только находим (t уст) при известном (Т=11,7)

Вывод: в данной лабораторной работе мы определяли переходные и частотные характеристики периодических звеньев. Так же были исследованы зависимости характеристик звеньев от параметров системы.

Для выполнения работы использовалась программа VisSim и Mathcad.

Дата добавления: 2015-09-05