Задача 1.6.

Вариант 1.

Даны 1-ый, 3-ий, 5-ый столбцы матрицы А. Построить 2-ой, 4-ый, 6-ой столбцы по формуле: а_ij = 2.5a_i,j-1 для j = 2, 4, 6. Вывести на печать полученную матрицу. 1 столбец = (5.1 8.7 9.3 14.4), 2 столбец = (7.3 9.8 14.2 3.4), 3 столбец = (2.4 7.2 11.9 3.3).

Вариант 2.

Дана матрица А. Из нее образовать две матрицы: в одной оставить все отрицательные элементы матрицы А (на месте положительных элементов поставить ноль), в другой матрице оставить все положительные элементы (на месте отрицательных поставить ноль).

Вариант 3.

Вычислить сумму элементов матрицы А (5,5), расположенных выше главной диагонали и удовлетворяющих условию: 1 < a_ij £ 2,5. Элементы матрицы сформировать по правилу: a_ij = i + 0,5j.

Вариант 4.

Построить матрицу В (5,4), каждый элемент которой находится по формуле: , где S_i – сумма элементов i -той строки матрицы А.

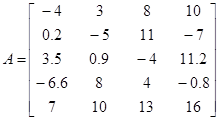
Вариант 5.

Сформировать матрицу С (5,5) по правилу: 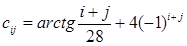. Найти сумму отрицательных элементов матрицы, расположенных ниже побочной диагонали (i, j = 1,…,5).

Вариант 6.

Сформировать матрицу В (9,9) по правилу: b_ij = cos(i) – sin(j). Подсчитать количество строк матрицы, начинающихся с отрицательного элемента.

Вариант 7.

Переписать первые элементы каждой строки матрицы А (7,3) в массив D, если в строке есть элемент больше 13. Если в строке нет такого элемента, то записать ноль в массив D в соответствующем месте. Вывести исходную матрицу и образованный массив на печать одновременно. Элементы матрицы А задать самостоятельно.

Вариант 8.

Определить суммы положительных элементов матрицы А для каждой строки, исключая элементы главной диагонали.

Вариант 9.

Подсчитать количество нулевых элементов среди элементов, расположенных выше главной диагонали матрицы В (8,8), которые формируются по правилу:

b_ij = cos – 16, (i, j = 1,…,8).

Вариант 10.

Найти сумму индексов отрицательных элементов матрицы В (4,4), расположенных выше побочной диагонали.

Вариант 11.

Найти среднее геометрическое элементов каждого чётного столбца и среднее арифметическое элементов каждого нечетного столбца матрицы.

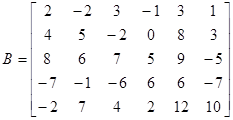
Вариант 12.

Умножить четные строки матрицы R на m = ½sin(k)½, где k – номер умножаемой строки. Полученную матрицу напечатать.

Вариант 13.

Построить вещественную матрицу A (10,10) по правилу: a_ij = cos (i² + 5).

Заменить нулями все ее элементы, расположенные на главной диагонали и выше нее. Вывести на печать для сравнения обе матрицы.

Вариант 14.

В исходной матрице найти количество четных элементов, больших 4, и нечетных элементов, меньших 67.

Вариант 15.

В исходной матрице заменить все элементы, по модулю меньшие 1, на 1. Подсчитать сумму элементов исходной и полученной матрицы отдельно. Отпечатать матрицу С после замены элементов.

Вариант 16.

В построенной матрице A (7,4) определить количество элементов, для которых выполнено условие: -0,5 < a_ij < 0,5. Элементы матрицы строятся по правилу: a_ij = sin (i + j / 2). Матрицу напечатать.

Вариант 17.

Найти произведение элементов главной диагонали и сумму элементов побочной диагонали матрицы В (6,6) и указать большее из двух найденных значений. Элементы матрицы формируются по правилу: b_ij = 2 ⁱ + j.

Вариант 18.

Дана матрица Z. Найти сумму элементов для каждого столбца, начинающегося с положительного элемента.

Вариант 19.

Определить сумму и количество элементов матрицы А (6,6), формирующихся по правилу: a_ij = cos (i + j), удовлетворяющих условию: 0.3 <= a_ij < 1, среди элементов, находящихся ниже побочной или выше главной диагонали.

Вариант 20.

Дана матрица Y (5,5) (элементы матрицы выбрать самостоятельно). Вычислить элементы новой матрицы Z (5,5) по правилу: z_ij = y_ij / k_i, где k_i – количество положительных элементов i – той строки. Если в i – той строке положительных элементов нет, то i – тая строка в матрице Z должна быть заполнена нулями. Отпечатать для сравнения обе матрицы Y и Z.

Вариант 21.

Вычесть из суммы элементов матрицы В (5,5), расположенных ниже главной диагонали, произведение элементов побочной диагонали.

Вариант 22.

Найти количество отличных от нуля элементов, расположенных ниже побочной диагонали. Нулевые элементы матрицы заменить на –1.

Вариант 23.

Для матрицы В определить количество четных элементов, расположенных на главной диагонали и выше неё. Элементы матрицы В формируются по правилу:

b_ij = 100×RND (1), (i, j = 1, 2, …, 5).

Примечание: элементы матрицы формируются случайным образом с помощью функции RND, генерирующей случайное число в диапазоне от 0 до 1.

Вариант 24.

С помощью элементов исходной матрицы А (5,5) построить новые матрицы С (5,5) и В (5,5), элементы которых находятся по правилу:

.

Вариант 25.

Дана матрица А (7,7) (элементы матрицы выбрать самостоятельно). Найти значение K= 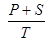, где: P –произведение положительных элементов матрицы А, S – сумма отрицательных элементов матрицы А, T – произведение элементов побочной диагонали.

Вариант 26.

Найти разность двух матриц и определить количество элементов, строго больших 2.5, среди элементов полученной матрицы.

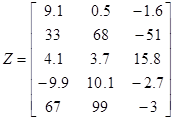
Вариант 27.

Определить суммы отрицательных элементов матрицы А (5,4) в каждой строке и напечатать матрицу А (5,5), в которой пятый столбец образован из полученных сумм.

.

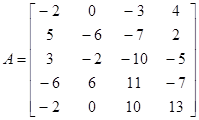Дата добавления: 2015-09-05