Задача 1.4.

Вариант 1.

Вычислить количество значений функции Y, удовлетворяющих условию: 5< Y <10. Значения функции Y вычисляются по формулам:

Вариант 2.

Вычислить значение функции , где

Вариант 3.

Вычислить значение . Значения функции z вычисляются при всех заданных значениях t из промежутка: t Î [2,6; 7,4], шаг h = 0,6.

Вариант 4.

Вычислить произведение значений функции Y по формуле: где

Вариант 5.

Вычислить значение 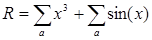, где x = 2,3a + ln (a)

для a Î [1; 4]; шаг h =0,2.

Вариант 6.

Подсчитать сумму значений функции Y, удовлетворяющих условию: Y < b², где для x [M1] Î [0,5; 5,5], шаг h = 0,5; g = 0,6; b = 1,62; a = 2,3.

Вариант 7.

Вычислить произведение для n Î [0; 1,5], шаг h = 0.1, где x = (2 + n)sin (n + 1).

Вариант 8.

Задана последовательность для x Î [-2,3; 0,5], шаг h = 0,2. Вычислить значение функции Y, равное удвоенной сумме всех положительных значений функции Z = -2,3x + sin x.

Вариант 9.

Вычислить произведени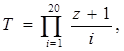е где , для y Î [1; 20], шаг h = 1.

Вариант 10.

Вычислить количество значений функции Y вида: удовлетворяющих условию: Y ³ cos (x) для x Î [5; 7], шаг h = 0,2.

Вариант 11.

Вычислить сумму и количество значений Z >1, если функция z вычисляется по формуле: для x Î [0,3; 2,7], шаг h = 0,3.

Вариант 12.

Вычислить значение: ,

где b = åa, y = 10,7 для a Î [4; 8,6], шаг h = 0,1; c = 0,3.

Вариант 13.

Вычислить значени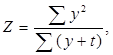е где 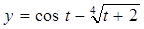для t Î [0,1; 0,5], шаг h = 0,05.

Вариант 14.

Вычислить - произведение положительных значений функции f = 2,7sin (x) – x для x Î [0,1; 5], шаг h = 0,2.

Вариант 15.

Вычислить значение:

,

Вариант 16.

Вычислить значение для x Î [-2; 5], шаг h = 0.5; a = 4.7; b = -3.5.

Вариант 17.

Вычислить произведение где:

для x = 0,784; k = 8,39.

Вариант 18.

Вычислить произведение квадратов отрицательных значений функции Y = sin (x + a) для x Î [-8; 10], шаг h = 2; a = 5.

Вариант 19.

Вычислить количество положительных значений функции 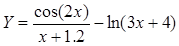и количество отрицательных значений функции Y. Вывести на печать наибольшее количество. Значения функции Y вычисляются для x Î [0,2; 3], шаг h = 0,2.

Вариант 20.

Вычислить сумму .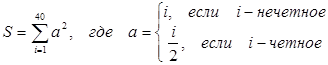

Вариант 21.

Вычислить значения функции для x Î [-1,3; 2,5], шаг h = 0,2. Все отрицательные значения функции Z увеличить на 0.5, а все неотрицательные -уменьшить на 1. Вычислить сумму полученных значений функции Z.

Вариант 22.

Вычислить значения функции Y = x² - 5 для x Î [-2; 26], шаг h = 2. Если среди значений Y есть число, равное a, то вычислить сумму всех значений Y, в противном случае вывести на печать значение “111” (Вычисления выполнять для a = 95).

Вариант 23.

Вычислить значение функции F = 2^x – sin (x) + x² для x Î [0,5; 4], шаг h = 0,3. Если количество значений F, меньших 10, окажется больше 5, то вывести на печать признак “ V ”, в противном случае отпечатать “ S ”.

Вариант 24.

Вычислить значения функции: для x Î [0,1; 2], шаг h = 0,2. Подсчитать количество значений P, больших 1, и количество значений P, меньших 1.

Вариант 25.

Вычислить значения функции: для i = 1, 2,…,15. Определить произведение положительных значений функции a.

Вариант 26.

Вычислить значения функции: Z = sin² (3k + 5) – cos (k² - 15) для k = 1, 2,…,12. Требуется определить, сколько у функции Z значений меньших 0.25, и найти их сумму.

Вариант 27.

Вычислить значение

Дата добавления: 2015-09-05