Москва, Волхонка, 14

^[1] Я имею в виду работы московского методологического кружка 60‑х - 70‑х г.г. (Г.П.Щедровицкий и др.), исследования по проблеме структуры и динамики науки, проводившиеся в 70-х годах в Институте философии АН СССР, в Институте истории естествознания и техники и в Институте системных исследований АН СССР (работы И.С.Алексеева, Л.Б.Баженова, П.Л.Гайденко, Г.Г.Горохова, З.З.Казютинского, Р.С.Карпинской, Е.А.Мамчур, Г.А.Лекторского, Г.Н.Рузавина, В.Н.Садовского, В.А.Смирнова, Ю.В.Сачкова, В.Н.Поруса, Б.Г.Юдина, В.С.Швырева и др.); труды киевских философов и методологов (П.С.Дышлевой, Б.С.Крымский, В.И.Кузнецов; М.В.Попович и др.); исследования ленинградских философов (М.В.Мостепаненко, Л.А. Микешина, А.С.Кармин); работы новосибирских методологов (М.А.Розов и др.), исследования минской методологической школы (В.С.Степин, Л.А.Томильчик и др.).

^[1] Кант И. Соч.: В 6 т. М.,1964. Т.3. С.261.

^[2] Reichenbach H. Wahrscheinlichkeitslehre. Leiden,1935. S.420.

^[3] Otto R. Das Heilige. Uber das Irrationale in der Idee des Göttlichen und sein Verhältnis zum Rationalen. München,1936.

^[4] Heisenberg W. Ueber den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik//Zeitschrift fr Physik.1927. B.43. S.197.

^[5] Ibid.

^[6] Ibid.

^[7] Stegmüller W. Das Problem der Kausalität/Probleme der Wissenschaftstheorie, Festschrift fr Victor Kraft. Vienna,1960. S.183.

^[8] Heisenberg W. Physikalische Prinzipien der Quantentheorie. Mannheim,1958. S.45.

^[9] Weizscker von C.F. Zum Weltbild der Physik. Stuttgart,1958. S.85 f.

^[10] Physical Review. 1952. Vol. 85. № 2. P. 187. Не столь важно, что данный пример, как и пример с копенгагенской школой, также можно отнести к разряду "исторических". Оба эти примера следует рассматривать как case studies*, в которых демонстрируются и подвергаются проверке некоторые фундаментальные теоретико-эпистемологические ориентации. Они также указывают на связь этих ориентаций с отдельными философскими концепциями. [* case studies - ситуативные эпистемологические исследования, часто тесно связанные с историко-научными данными (Перев.)].

[11] Physical Review. 1952. Vol. 85. № 2. P. 166 и далее; Progress of Theoretical Physics, 1953, vol.9, №3, p.273 и далее; Physical Review, 1954, vol.96, №1, p.208.

^[12] Heisenberg W. The Development of the Interpretation of the Quantum Theory // Niels Bohr and the Development of Physics. L., 1955. P.17 и далее.

[13] Bohm D. Causality and Chance in Modern Physics, L., 1958. P.170.

^[14] Heisenberg W. The Development of the Interpretation of the Quantum Theory, P.18.

^[15] Вычленив достаточно большое число эквивалентных систем и подвергнув статистической обработке данные, можно получить следующую результирующую разность:

,

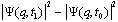которая выступает как аппроксимация:

.

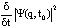Применяя специальные математические методы, можно вывести -функцию, удовлетворяющую статистическому значению:

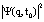и ,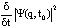

и в то же время представляющую решение второго уравнения Шредингера.

В таком случае можно говорить об "экспериментально определенной" -функции. Такого рода определенность указывает на то, что она возможна лишь как некое грубое приближение и не допускает точного измерения.

^[16] Против этого может быть выдвинуто возражение в духе эмпирицизма, что, дескать, подобная формулировка основывается на слишком узком, а потому неудовлетворительном понятии эмпирической проверяемости. Если принять аргументацию, развитую в работе Карнапа "Теоретические понятия науки" (Theoretische Begriffe der Wissenschaft // Zeitschrift fr Philosophische Forschung. 1960. Vol. 14. P. 209 и далее), то некоторая комбинация универсальных и экзистенциальных предложений, подобных принципу причинности, могла бы также считаться "эмпирически значимой", то есть обладать определенным эмпирическим содержанием.

Я не имею возможности здесь входить в детали рассуждений Карнапа, приведенных в данной работе. Однако позволю себе лишь небольшое замечание: в этой работе Карнап явно отошел от своих более ранних требований, получивших большую известность после его знаменитой работы "Проверяемость и значение" (Carnap R. Testability and Meaning // Philosophy of Science, 1936-37, vol.3-4), состоявших в том, что все теоретические предикаты и предложения должны редуцироваться либо полностью, либо частично к непосредственно наблюдаемым. Теперь вместо этого его критерий "эмпирической значимости" звучит следующим образом: теоретическое понятие значимо, если его применение в "частной гипотезе" приводит в итоге к предсказыванию некоторого наблюдаемого события. Таким путем это понятие входит в "теоретический язык", который посредством "правил соответствия" может быть косвенно связан с предложениями о непосредственно наблюдаемом, от которых теоретический язык строго отграничен. (Это концепция, которая, по-моему, основывается на совершенно правильном анализе научной теории).

Вообще говоря, Карнап поступает правильно, сменив исходную позицию, отказавшись от ригористического деления на теоретическое и перцептуальное в пользу практических требований науки. Но в таком случае позволительно спросить: что же собственно эмпирицистского остается в его критерии значимости? Больше нельзя говорить о полной или частичной редукции теоретических понятий к наблюдаемым предикатам; решающим фактором становится то, получают ли теоретические понятия роль соучастия в предсказаниях вместе с предложениями наблюдения, теоретическими постулатами и правилами соответствия. Но тогда эти понятия являются порождениями мышления, а не ощущений, и, следовательно, не имеют чисто эмпирической природы.

Итак, мы видим, что эта работа Карнапа есть не улучшение эмпирицистской позиции, выраженной в "Проверяемости и значении" и свойственной Венскому кружку, а скорее является определенным отречением от этой позиции.

Таким образом, упомянутое ранее возражение, основанное на том, что идеи работы Карнапа "Теоретические понятия науки" позволяют считать принцип причинности эмпирически значимым и практически верифицируемым, следует отвести. Я утверждаю, что это возражение основывается на неправильном употреблении понятия "эмпирическое". Теперь мы видим, что в отличие от более ранних работ эта статья Карнапа свидетельствует о его признании решающего значения спонтанности мышления, которое стимулируется, но не детерминируется наблюдениями во всей области науки (а не только в сфере логики).

В этой связи важно понять, что имеет в виду Карнап, когда говорит о "реальном" объяснении в науке, а именно: лишь то, что теория признается до тех пор, пока ее постулаты вместе с правилами соответствия могут использоваться для направления ожиданий исследователя, точнее, для выведения предложений наблюдения, которыми выражаются эти ожидания. Следовательно, "реальное" для него - это то, что применимо для достижения поставленных целей, а не то, что теоретически основывается на ощущениях.

См. также: Stegmüller W. Das Problem der Kausalität // Probleme der Wissenschaftstheorie, Festschrift fr Victor Kraft. Vienna, 1960. S. 87; Pap A. Analytische Erkenntnistheorie. Vienna, 1955. S. 138 и далее.

^[17] См.: Пуанкаре А. Наука и гипотеза // Пуанкаре А. О науке. М., 1983. С. 5-152; Энштейн А. Геометрия и опыт // Эйнштейн А. Собрание научных трудов. М., 1967. Т. 2. С. 83-94; Грюнбаум А. Философские проблемы пространства и времени. М., 1969; Riemann B. Ueber die Hypothesen, welche der Geometrie zugrunde liegen Gottingen,1892; Dingler H. Relativittstheorie und konomienprinzip. Leipzig, 1922; Reihenbach H. Philosophie der Raum-Zeit-Lehre. Berlin, 1928.

^[18] См.: Duhem P. La theorie physique: Son objet, sa structure. P., 1914; Cassirer E. Das Erkenntnisproblem in der Philosophie und Wissenschaft der neueren Zeit von Hegels Tod bis zur Gegenwart. Stuttgart, 1957; Carnap R. Theoretische Begriffe der Wissenschaft // Zeitschrift fr philosophische Forschung, 1960.

^[19] У нас всегда есть лишь конечное число n отдельных измерений, результат каждого из которых отличается от остальных: l ₁, l ₂,..., l _n; но мы не располагаем "истинным значением" X, существование которого определяется правилом. Пусть e_k = l_k -X - это отклонение частных результатов от предполагаемого "истинного значения" X. Допустим, далее, что погрешность измерения с равной вероятностью может быть со знаком "+" и со знаком "-" (т.е. ее алгебраическая сумма аппроксимирует к крайнему пределу), тогда истинная средняя погрешность для частного l _k вычисляется по формуле:

.

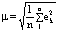Наконец, сделаем еще одно допущение, что среднее арифметическое отдельных значений - назовем его оптимальным значением L - наиболее близко подходит к истинному значению. Тогда, взяв v_k = l _k - L как среднюю погрешность по отношению к L, получим

.

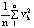Применяя все эти неэмпирические правила, мы с помощью простых преобразований приходим к уравнению:

,

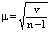где .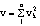

Дата добавления: 2015-09-04