Примеры 1 - 6

1. Пусть Z = (Z; +) - аддитивная абелева бесконечная группа целых чисел, а Z_чет. подмножество четных целых чисел. Покажем, что тогда алгебра Z _чет. = (Z_чет.; +) является подгруппой группы Z. Проверим выполнение условий критерия 1:

1) (" z ₁, z ₂ÎZ_чет. )[ z ₁+ z ₂Î Z_чет.];

2) (" z ÎZ_чет.)[- z ÎZ_чет.].

Следовательно, Z _чет.= (Z_чет.; +) p Z = (Z; +).

2. Подмножество нечетных чисел Z_неч. множества целых чисел Z не образует подгруппу группы Z = (Z; +), так как нарушается первое условие первого критерия подгруппы:

(" z ₁, z ₂Î Z_неч.)[ z ₁ + z ₂ ÎZ_чет.].

3. Вообще, имеется следующая цепочка подгрупп и групп:

Z _чет. = (Z_чет.; +) p Z = (Z; +) p Q= (Q; +)p R= (R; +) p C= (C; +).

4. Подмножество всех параллельных переносов T множества движений D плоскости p образует подгруппу T= (T; ×) группы D = (D; ×). В самом деле, выполняются условия:

1) (" t ₁, t ₂Î T)[ t ₁× t ₂Î T ];

2) (" t Î T)[ t^{- 1}Î T ].

Аналогично показывается, что подмножество всех вращений R _o^a множества движений D плоскости p образует подгруппу R_o^a = (R _o^a; ×) группы D= (D; ×).

5. Подмножество четных подстановок n -го порядка А_n множества всех подстановок n -го порядка S_n образует подгруппу A _n = (A_n; ×) группы S _n = (S_n; ×), так как: 1) произведение двух четных подстановок n -го порядка является четной подстановкой n -го порядка; 2) обратная подстановка к четной подстановке n -го порядка также есть четная подстановка n -го порядка. Подгруппа À _n называется знакопеременной группой n- ой степени (порядок этой группы равняется ).

6. Показать, что множество матриц вида М _2х2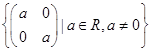^*= относительно умножения образует подгруппу мультипликативной группы Ì_2х2 всех невырожденных матриц 2-го порядка.

Доказательство. Пусть А ^* - любая матрица из М _2х2^*, следовательно, a ¹ 0. Но тогда ô А ^*ô = a ² ≠ 0, а потому А ^* является невырожденной матрицей, то есть множество М _2х2^* Ì М _2х2.

Проверим теперь выполнение условий 1) - 2) первого критерия подгруппы.

1) Пусть А ^*= , В ^*= - любые матрицы из М _2х2^*. Поскольку a ≠ 0, b ≠ 0, то ab ¹ 0. Тогда А ^* В ^* = , где ab Î R и ab ¹ 0. Поэтому А ^* В ^*Î М _2х2^*.

2) Для матрицы А ^*= из М _2х2^* обратной является матрица

(А ^*)^-1= , при этом ¹ 0, а потому (А ^*)^-1 Î М _2х2^*.

Из условий 1) и 2) следует, что Ì_2х2^* = (М _2х2^*; ×) есть подгруппа группы Ì_2х2.

п.2. Простейшие свойства подгрупп. Пусть G = (G; *)-некоторая группа, а G₁ = (G ₁; *) - ее подгруппа. Согласно первому критерию подгруппы, подмножество G ₁ замкнуто относительно бинарной операции * в группе G, то есть применение этой операции к элементам из G ₁ приводит снова к элементу из G ₁. Кроме того, бинарная операция подгруппы G₁ является ограничением соответствующей операции группы G множеством G ₁. Если обозначим бинарную операцию на G ₁ через */ _G , то

(" g ₁, g ₂Î G)[ g ₁, g ₂ Î G ₁Þ g ₁ */ _G g ₂ = g ₁* g ₂]. (1)

Приведем простейшие свойства подгрупп.

1^°. Любая подгруппа группы является группой. Нейтральный элемент группы является нейтральным элементом любой ее подгруппы.

Доказательство. Пусть G ₁ = (G ₁; *) - подгруппа группы G = (G; *) и е - нейтральный элемент группы G. Согласно определению 1 и условию (1), алгебра G ₁ = (G ₁; *) является группой.

Элемент е Î G ₁, так как в силу (1) для любого элемента g ₁Î G ₁ имеем

e= g ₁* s (g ₁) = g ₁ */ _G s (g ₁)Î G ₁.

Кроме того, е Î G ₁ удовлетворяет условиям

e * g ₁ = e */ _G g ₁ = g ₁ и g ₁ * e= g ₁*/ _G e= g ₁,

то есть е является нейтральным элементом относительно бинарной операции *.

ч.т.д.

Пусть */ _G -ограничение бинарной операции * группы G множеством G ₁, то есть выполняется условие (1). По свойству 1°

G ₁= (G ₁; */ _G ) p G = (G; *). Таким образом, подгруппа G ₁ группы G однозначно определяется непустым подмножеством G ₁, замкнутым в G относительно бинарной операции *. Поэтому вместо записи

G₁= (G ₁; */ _G ) p G = (G; *) пишут: " подгруппа G ₁= (G ₁; *)" или говорят: " подмножество G ₁ образует подгруппу группы G относительно бинарной операции * ", или иногда говорят: " подмножество G ₁ является подгруппой группы G относительно бинарной операции * ". Заметим, что последнее выражение является некорректным, так как при этом смешиваются понятия "множество" и "алгебра".

2^°. Бинарное отношение "быть подгруппой" на множестве всех подгрупп данной группы является отношением нестрого порядка.

Доказательство. Это свойство подгрупп является частным случаем такого же свойства, доказанного для подалгебр.

ч.т.д.

Пересечение любых двух подгрупп G ₁ и G ₂ группы G имеет непустое основное множество G ₁Ç G ₂ , так как, по крайней мере, оно содержит нейтральный элемент е, согласно свойству 1°.

3^°. Пересечение произвольной совокупности (конечной или бесконечной) подгрупп группы G также является подгруппой этой группы.

Доказательство. Не умаляя общности рассуждений, докажем это свойство для пересечения двух подгрупп G ₁ = (G ₁; *) и G ₂ = (G ₂; *) группы G = (G; *). Действительно, если g ₁, g ₂Î G ₁Ç G ₂, то g ₁Î G ₁, g ₂Î G ₁ и g ₁Î G ₂, g ₂Î G ₂. Поэтому по условию 1) критерия 1, также g ₁* g ₂Î G ₁ и g ₁* g ₂Î G ₂, а по определению пересечения Ç получаем g ₁* g ₂Î G ₁Ç G ₂ . По условию 2) критерия 1 s (g ₁), s (g ₂)Î G ₁ и s (g ₁), s (g ₂)Î G ₂, а по определению пересечения Ç получаем s (g ₁), s (g ₂)Î G ₁Ç G ₂.

Итак, по первому критерию подгруппы, алгебра G ₁ÇG ₂ = (G ₁Ç G ₂; *) является подгруппой группы G.

ч.т.д.

Очевидно, что пересечением всех подгрупп группы G будет тривиальная подгруппа E = ({ e }; *).

п.3. Порождающие элементы и множества группы. Циклическая подгруппа элемента. Пусть Н - произвольное непустое подмножество множества G группы G = (G; *). Из свойства 3^° следует, что для множества Н существует наименьшая подгруппа H, содержащая множество Н. Нетрудно убедиться, что H является пересечением всех подгрупп группы G,содержащих Н (рис.3.1).

ОПРЕДЕЛЕНИЕ 2. Наименьшая подгруппа H, содержащая непустое подмножество Н множества G группы G называется подгруппой, порожденной множеством Н, а Н - множеством образующих или системой образующих группы H.

Подгруппа, порожденная множеством Н, обозначается через (H) или { H }.

G C C

Рис. 3.1. Рис. 3.2.

Если подмножество Н состоит только из одного элемента g _o, то порожденная им подгруппа (g _o) называется циклической подгруппой элемента g _o. К подгруппе (g _o) принадлежат, конечно, все композиции g _o, где k Î Z, элемента g _o.

Дата добавления: 2015-08-27