Process of sampling

Consider a continuous time signal 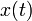. Its one sided Laplace transform is defined as: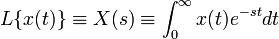

If the continuous time signal 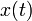is uniformly sampled with a train of impulses to get a discrete time signal 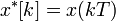, then it can be represented as:

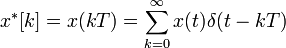
where 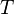is the sampling interval.

Now the Laplace transform of the sampled signal (discrete time) is called Star transform and is given by:

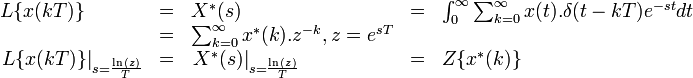
It can be seen that the Laplace transform of an impulse sampled signal is the star transform and is the same as the Z transform of the corresponding sequence when 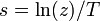. Similar relationship holds when a continuous time system is converted into a sampled data system by cascading an actual impulse sampler at the input and a fictitious impulse sampler at the output.^[7]

Дата добавления: 2015-08-27