Region of convergence

The region of convergence (ROC) is the set of points in the complex plane for which the Z-transform summation converges.

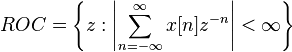
Example 1 (no ROC)

Let 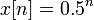. Expanding 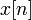on the interval 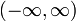it becomes

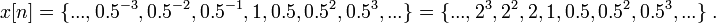
Looking at the sum

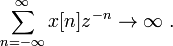
Therefore, there are no values of that satisfy this condition.

Example 2 (causal ROC)

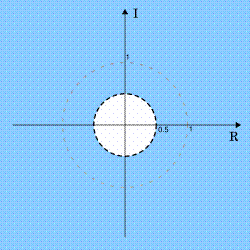
ROC shown in blue, the unit circle as a dotted grey circle (appears reddish to the eye) and the circle 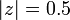is shown as a dashed black circle

Let 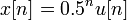(where 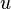is the Heaviside step function). Expanding 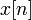on the interval 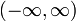it becomes

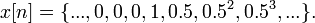
Looking at the sum

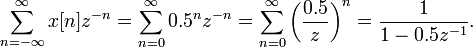
The last equality arises from the infinite geometric series and the equality only holds if 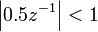which can be rewritten in terms of 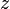as 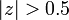. Thus, the ROC is 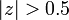. In this case the ROC is the complex plane with a disc of radius 0.5 at the origin "punched out".

Example 3 (anticausal ROC)

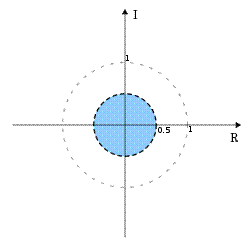
ROC shown in blue, the unit circle as a dotted grey circle and the circle 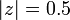is shown as a dashed black circle

Let 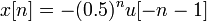(where 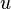is the Heaviside step function). Expanding 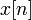on the interval 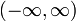it becomes

Looking at the sum

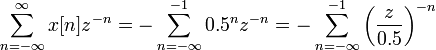
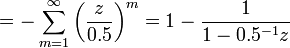
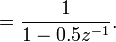
Using the infinite geometric series, again, the equality only holds if 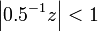which can be rewritten in terms of 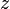as 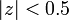. Thus, the ROC is 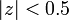. In this case the ROC is a disc centered at the origin and of radius 0.5.

What differentiates this example from the previous example is only the ROC. This is intentional to demonstrate that the transform result alone is insufficient.

Дата добавления: 2015-08-27