Приклад алгоритму та програми. Знайти корені нелінійного рівняння виду

Знайти корені нелінійного рівняння виду . Пошук наближеного значення хоча б одного кореня рівняння f (x) = 0 на відрізку [ a; b ] здійснюватимемо методом ділення відрізка навпіл. Для цього обчислимо середину m відрізка, і якщо f (m)¹0, то пошук продовжуватимемо на тому з відрізків [ a; m ], [ m; b ], на кінцях якого функція приймає значення різних знаків. Реалізація алгоритму подана у програмі ex5_5. Для обчислення значення функції в заданій точці визначимо функцію f(xx). У програмі змінюватимуться значення змінних через розименування покажчика, наприклад, *a = x, де double* const a — константний покажчик на тип double, double x — змінна, на яку посилатиметься покажчик. Спроба змінити сам покажчик приведе до синтаксичної помилки.

//ex6_1.срр пошук кореня рівняння методом ділення відрізка навпіл
#include<iostream>
#include<math.h>
using namespace std;
double precision=0.00001,x; //точність та аргумент функції
//========== обчислити значення функції в точці ===============
double f(double *param)
{
if (*param==0) //перевірити точку розриву,
*param+=precision; //перейти до наступної точки
return exp(*param)-1/(*param);//значення функції в поточній точці
}
//=====реалізація алгоритму половинного ділення ================
void solution(double* a, double* b)
{ //параметри - константні покажчики на границі відрізка
do{
x=(*a+*b)/2; //визначити середину відрізка
if (f(&x)*f(&(*a))<0) //знаки функції різні на кінцях відрізка
*b=x; //вибрати новий кінець відрізку
else *a=x;
}while((*b-*a)>=precision); //точність розрахунків досягнута
}

//======================= головна функція =====================
int main(){
double left,right; //границі відрізка
cout<<"pointer to data"<<endl;
cout<<"define root of e^x=1/x"<<endl;
cout<<"input a,b"<<endl;
cin>>left>>right; //ввести значення кінців відрізка
double* pl=&left;//ініціалізувати константні покажчики
double* pr=&right;
solution(pl,pr); //розв’язати рівняння
cout<<"root = "<<x<<endl; //вивести значення кореня рівняння
system("pause");
}

Рис. 6.1. Результат роботи програми ex6_1.
Розв’язання нелінійного рівняння

6.3. Варіанти завдань

1. Надрукувати таблиці значень функцій cox(x) та e ^x на відрізку [ a; b ] із кроком h, розвинувши функції у ряд Тейлора та використавши покажчики на функції. Для довідки: ряд Тейлора для функції сos(x) =1 – x ²/2! + x ⁴/4! – x ⁶ /6! +..., ряд Тейлора для функції e ^x =1 + x / 1! + x ² / 2! + x ³ / 3! +...

2. Розрахувати біноміальні коефіцієнти: C (m, n) = 1, якщо m £ 1, n = 0 або n = m; C (m, n) = C (m – 1, n – 1) + C (m – 1, n) в протилежному випадку. Значення n та m передавати у функцію як покажчики на тип int.

3. Нехай в трикутнику ABC задані координати вершин A =(0,0), B =(а,b), де а і b – цілі числа, що вводяться користувачем. Розробити функцію, яка визначає такі координати вершини C =(x, y), щоб площа трикутника ABC була мінімальною (не рівною нулю). Координати вершин передавати у функцію як покажчики на тип int.

4. Вивести в порядку зростання всі звичайні нескоротні дроби в діапазоні від 0 до 1, знаменники яких не перевищують 15. Чисельники та знаменники дробів подати як покажчики на типи int

5. Написати програму, яка здійснює введення у вільному форматі одного цілого числа і його переведення з текстового представлення в значення типу int. Функція getint() повинна повертати значення отриманого числа через параметр або сигналізувати значенням, якщо вхідний потік вичерпаний. Значення EOF повертати через оператор return. Знаки - або +, за якими не йде цифра, функція розуміє як неправильне представлення числа.

6. Розв’язати нелінійне рівняння x =cos(x) методами перебору та хорд, визначивши інтервал [ a, b ], на якому існує рішення рівняння. Порівняти результати розв’язків двома методами. У функції, що реалізують алгоритми, передавати покажчики на тип float.

7. Знайти корені нелінійного рівняння виду . Пошук наближеного значення хоча б одного кореня рівняння f (x) = 0 на відрізку [ a; b ] здійснювати методами перебору та дотичних. У функції, що реалізують алгоритми, передавати покажчики на тип float.

8. Знайти корені нелінійного рівняння виду . Пошук наближеного значення хоча б одного кореня рівняння f (x) = 0 на відрізку [ a; b ] здійснювати методами перебору та хорд.У функції, що реалізують алгоритми, передавати покажчики на тип float.

9. Знайти корені нелінійного рівняння виду . Пошук наближеного значення хоча б одного кореня рівняння f (x) = 0 на відрізку [ a; b ] здійснювати методами перебору та хорд. У функції, що реалізують алгоритми, передавати покажчики на тип float.

10. Знайти корені нелінійного рівняння виду . Пошук наближеного значення хоча б одного кореня рівняння f (x) = 0 на відрізку [ a; b ] здійснювати методами перебору та хорд. У функції, що реалізують алгоритми, передавати покажчики на тип float

11. Знайти корені нелінійного рівняння виду . Пошук наближеного значення хоча б одного кореня рівняння f (x) = 0 на відрізку [ a; b ] здійснювати методами дотичних та хорд. У функції, що реалізують алгоритми, передавати покажчики на тип float

12. Знайти корені нелінійного рівняння виду . Пошук наближеного значення хоча б одного кореня рівняння f (x) = 0 на відрізку [ a; b ] здійснювати методами дотичних та ділення навпіл. У функції, що реалізують алгоритми, передавати покажчики на тип float

13. Використовуючи покажчики на функції для їх викликів, знайти найбільше, найменше та середнє арифметичне значення двох чисел, які генеруються комп’ютером.

14. Використовуючи покажчики на функції для їх викликів, обчислити ланцюговий дріб

15. Використовуючи покажчики на функції для їх викликів, обчислити ланцюговий дріб

16. Використовуючи покажчики на функції для їх викликів, обчислити ланцюговий дріб

17. Скласти програму обчислення найбільшого числа Фібоначчі, яке не перевищує число 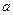та номера найменшого числа Фібоначчі, яке більше від числа 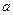. Використати функції, що повертають покажчики на тип int.

18. Число називається досконалим, якщо воно дорівнює сумі всіх своїх дільників, крім самого цього числа. Використати функцію, що повертає покажчик на тип int, в якому зберігається досконале число з проміжку [2, n ]. Надрукувати досконалі числа з проміжку [2, n ], котрі є повними квадратами.

19. Скласти програму для знаходження всіх простих чисел із діапазону [2, n ], які є числами послідовності Фібоначчі або числами виду , де q – ціле число. Для обчислення простих чисел використати функцію, яка повертає значення типу покажчик на цілий тип та приймає покажчики.

20. Послідовність задана рекурентним співвідношенням

Для знаходження найбільшого члена цієї послідовності та його номера, який не перевищує число а, використати функцію, що повертає покажчики на типи int знайдених значень.

21. Скласти програму обчислення числа p за формулою Грегорі

та за формулою Валліса , використовуючи покажчики для повернення значень з функцій обчислення числа p. Розрахувати кількість ітерацій в каждому з методів.

22. Задати натральне число . Визначити, чи можна його подати у вигляді суми квадратів двох натуральних чисел. Якщо можливо, то визначити вказати пару 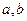таких натуральних чисел, що . Використати функції, що повертають покажчики на цілий тип та використовують покажчики як параметри.

23. Задати натуральне число . Знайти усі менші за паліндроми, які при піднесенні до квадрата дають також паліндром. Число є паліндромом, якщо його можна прочитати справа наліво та зліва направо однаково, наприклад, 12321.Використати функції, що повертають покажчики на цілий тип та використовують покажчики як параметри.

24. Скласти програму визначення чисел Армстронга, що складаються з двох, трьох та чотирьох цифр. Натуральне число із цифр є числом Армстронга, якщо сума його цифр, піднесених до го степеня, дорівнює самому числу, наприклад, 153=1³+5³+3³. Використати функції, що повертають покажчики на цілий тип та використовують покажчики як параметри.

6.4 Контрольні запитання

1. Дати поняття посилальних типів даних?

2. Як здійснюється до доступ до значення змінної?

3. Як оголосити покажчик на певний тип та посилання на змінну?

4. Як ініціалізувати покажчик та посилання?

5. Що відбувається під час звернення до неініціалізованого покажчика?

6. Які значення можна присвоювати покажчику?

7. Які операції припустимі для покажчиків?

8. Що таке «розименування покажчика»?

9. Як змінюється значення покажчика при додаванні чи відніманні цілого числа?

10. У чому полягає особливість покажчиків типу void*?

11. Як використовують покажчики на функції?

Одновимірні масиви
Лабораторна робота 7

Мета роботи.

¾ ознайомитися з особливостями типу масиву;

¾ опанувати технологію застосування масивів даних;

¾ навчитися розробляти алгоритми та програми із застосуванням одновимірних масивів

7.1 Теоретичні відомості

Тип масиву — це структурований тип даних, множина допустимих значень котрого складається з усіх масивів, для яких зафіксовано:

– розмірність;

– базовий тип;

– індексний тип;

– множину значень індексу.

З точки зору математики одновимірний масив — це вектор. Змінну, що матиме тип масиву, можна оголосити з використанням такого синтаксису:

<тип елементів> <ім’я масиву> [<кількість елементів>];

Основні властивості масивів:

– однорідність — усі елементи належать одному типу;

– сталість — вимірність масиву задається під час його оголошення і не змінюється протягом роботи з ним;

– рівнодоступність — спосіб доступу до всіх елементів є однаковим;

– послідовність розташування — усі елементи масиву розташовані в послідовних комірках оперативної пам’яті;

– індексованість — елементи однозначно ідентифікуються своїми індексами;

– упорядкованість індексу — індексний тип має бути простим порядковим типом даних.

Базовими операціями обробки масивів є:

– введення та виведення масиву;

– ініціалізація масиву;

– копіювання масиву;

– пошук максимального або мінімального елемента;

– обчислення узагальнювальних характеристик (сум елементів, їх добутків);

– пошук заданого елемента;

– перестановка елементів або обмін значеннями між елементами масиву;

– вставка та видалення елемента.

Базові операції обробки масивів зручно реалізовувати у вигляді функцій, що згодом можуть бути використані як «архітектурні блоки» при розв’язанні більш складних задач.

//ввести масив

for(i=0;i<n;i++)
cin>>mas[i];
cout<<"Entered array"<<endl;

//вивести масив
for(i=0;i<n;i++)
cout<<mas[i]<<" ";
cout<<endl;

//генерація масиву

srand((unsigned)time(NULL)); //ініціалізація генератора
//випадкових чисел
for(i=0;i<n;++i) //генерація псевдовипадкових чисел в діапазоні
mas[i]=rand()%30; //від 0 до 29

// пошук максимального елемента

max=mark[0]; //максимальної
for(i=1;i<n;i++) //пошук мінімальної та максимальної оцінок
{
if (max<mark[i]) max=mark[i]; //модифікація
//поточного максимуму
}

//бульбашкове сортування

for(i=0;i<n-1;i++)

for(j=i+1;j<n;j++)

if (mas[i]>mas[j])

{

tmp=mas[i];

mas[i]=mas[j];

mas[j]=tmp;

}

Дата добавления: 2015-08-27