Код програми. #include <stdio.h> //підключення бібліотек уведення-виведення

// |e^x - e^x/2, if -2 ≤ x ≤ 2

// Y={

// |e^(x+3)+1, if x < -2

// x between -5, 5, step 1

//e^x=1 + x / 1! + x2 / 2! + x3 / 3! +...

#include <stdio.h> //підключення бібліотек уведення-виведення

#include <conio.h>

#include <math.h> //підключення бібліотек математичних функцій

float y, //вираз за формулою Тейлора

st, //значення стандартної функції exp()

x, //аргумент функції

xn, xk, //початкове, кінцеве значення аргументу

xs, err, //крок зміни аргументу та похибка

t; //точність розрахунків

bool flag=true; // прапорець для визначення можливості
//розрахунку функції

//////// обчислення експоненти за формулою Тейлора /////////

double expon(float a)

{ //e^a=1 + a^1 / 1! + a^2 / 2! + a^3 / 3! +...

//параметр a - аргумент функції e^a

float sum=1; //сума членів ряду

int i=1; //знаменник елемента ряду

float member=1; //поточний елемент ряду

while (member>t) //поки поточний елемент перевищує

{ //точність розрахунків

member*= a/i; //поточний елемент за

// формулою Тейлора

sum+=member; //накопичення суми

i++;

} //перехід до нового елемента ряду

return sum; //повернення значення експоненти з функції

}

/////////////////// основна функція //////////////////////

int main (void)

{

puts("lab4: calculation exponention function");

printf("\n input xn, xk, xs (-5 5 1)\n");

scanf("%f%f%f", &xn, &xk, &xs);

printf("\n input t \n");

scanf("%f", &t);

puts("===================================================");

printf(" x y standart error \n");

puts("===================================================");

for (x=xn;x<=xk;x+=xs) //цикл перебору значень аргументів функції

{ if (x>=-2&&x<=2) //перевірка умов вибору

{ //розрахункової функції

y=expon(x)-expon(x/2); //визначення функції за

// формулою Тейлора

st=exp(x)-exp(x/2); //визначення функції за

//стандартною формулою

err=fabs(st - y); //розбіжності між точним і

//наближеним значеннями функції

}

else if (x<-2)

{

y=expon(x+3)+1;

st=exp(x+3)+1;

err=fabs(st-y);

}

else if (x>2) flag =false; // функцію не визначено

if (flag) //якщо функцію визначено, то вивести

// її значення

printf (" %f %f %f %f \n", x, y, st, err);

else printf (" %f not define \n", x);
//функцію не визначено

}

getch();

}

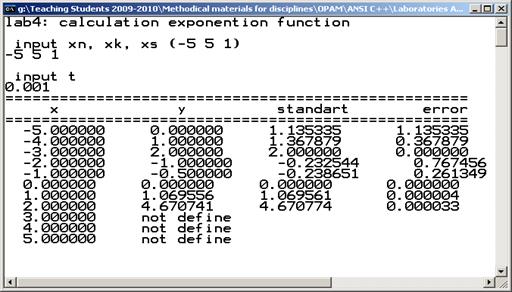
Рис. 4.1. Результати роботи програми ex4.1

4.3. Варіанти завдань

1. Обчислити значення функції у, розвинувши функцію cos(x) у ряд Тейлора. Аргумент х змінюється від -2 до 2 з кроком 0.5. Визначити похибку.

2. Обчислити значення функції у, розвинувши функцію у ряд Тейлора. Аргумент х змінюється від -2 до 2 з кроком 0.5. Визначити похибку.

3. Обчислити значення функції у, розвинувши функцію е-х у ряд Тейлора. Аргумент х змінюється від -2 до 2 з кроком 0.5. Визначити похибку.

4. Обчислити значення функції у, розвинувши функцію sin(x) у ряд Тейлора. Аргумент х змінюється від -2 до 2 з кроком 0.5. Визначити похибку.

5. Обчислити значення функції у, розвинувши функцію ln(x) у ряд Тейлора. Аргумент х змінюється від -1 до 3 з кроком 0.5. Визначити похибку.

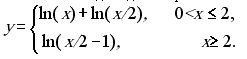
6. Обчислити значення функції у, розвинувши функцію arctg(x) у ряд Тейлора. Аргумент х змінюється від 0 до 3 з кроком 0.5. Визначити похибку.

7. Обчислити значення функції у, розвинувши функцію sh(x) у ряд Тейлора. Аргумент х змінюється від 0 до 3 з кроком 0.5. Визначити похибку.

8. Обчислити значення функції у, розвинувши функцію e^x у ряд Тейлора. Аргумент х змінюється від -2 до 2 з кроком 0.5. Визначити похибку.

9. Обчислити значення функції у, розвинувши функцію ln(x) у ряд Тейлора. Аргумент х змінюється від -2 до 2 з кроком 0.5. Визначити похибку.

10. Обчислити значення функції у, розвинувши функцію sin(x) у ряд Тейлора. Аргумент х змінюється від -2 до 2 з кроком 0.5. Визначити похибку.

11. Обчислити значення функції у, розвинувши функцію cos(x) у ряд Тейлора. Аргумент х змінюється від -2 до 2 з кроком 0.5. Визначити похибку.

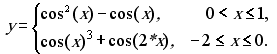
12. Обчислити значення функції у, розвинувши функцію e^-x у ряд Тейлора. Аргумент х змінюється від -2 до 2 з кроком 0.5. Визначити похибку.

.

13.Обчислити значення функції у, розвинувши функцію у ряд Тейлора. Аргумент х змінюється від -2 до 2 з кроком 0.5. Визначити похибку.

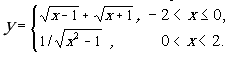
14. Обчислити значення функції у, розвинувши функцію tg(x) у ряд Тейлора. Аргумент х змінюється від -3 до 3 з кроком 0.5. Визначити похибку.

15. Обчислити значення функції у, розвинувши функцію cos(x) у ряд Тейлора. Аргумент х змінюється від -2 до 3 з кроком 0.5. Визначити похибку.

16. Обчислити значення функції у, розвинувши функцію sin(x) у ряд Тейлора. Аргумент х змінюється від -3 до 3 з кроком 0.5. Визначити похибку.

. 17. Обчислити значення функції у, розвинувши функцію tg(x) у ряд Тейлора. Аргумент х змінюється від -3 до 3 з кроком 0.5. Визначити похибку.

18. Обчислити значення функції у, розвинувши функцію sh(x) у ряд Тейлора. Аргумент х змінюється від -2 до 2 з кроком 0.5. Визначити похибку.

19. Обчислити значення функції у, розвинувши функцію cos(x) у ряд Тейлора. Аргумент х змінюється від -3 до 3 з кроком 0.5. Визначити похибку.

20. Обчислити значення функції у, розвинувши функцію sh(x) у ряд Тейлора. Аргумент х змінюється від -2 до 2 з кроком 0.5. Визначити похибку.

21. Обчислити значення функції у, розвинувши функцію e^-x у ряд Тейлора. Аргумент х змінюється від -2 до 2 з кроком 0.5. Визначити похибку.

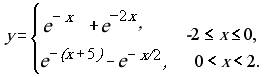
23. Обчислити значення функції у, розвинувши функцію tg(x) у ряд Тейлора. Аргумент х змінюється від -3 до 3 з кроком 0.5. Визначити похибку.

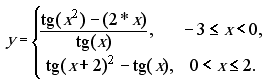
24. Обчислити значення функції у, розвинувши функцію ln(x) у ряд Тейлора. Аргумент х змінюється від -2 до 4 з кроком 0.5. Визначити похибку.

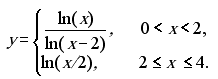
25. Обчислити значення виразу, використавши ряди для визначення констант pi та е: pi/4 = 1 - 1/3 + 1/5 - 1/7 + 1/9 -…; e = 1 + 1/1! + 1/2! + 1/3! +….

Визначити похибку обчислень.

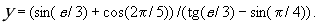
4.4 Контрольні запитання

1. Що таке ітераційний цикл?

2. Які причини зациклювання програм?

3. За яких умов цикл не виконується?

4. У чому полягають особливості застосування операторів break та continue?

5. Яке призначення функцій С++? Яка роль функції main()?

6. Що таке прототип функції? Що таке визначення функції?

7. Дати поняття рекурсивних функцій. Технологія припинення рекурсивного виклику.

8. Чим пряма рекурсія відрізняється від непрямої?

9. Якими бувають оператори виклику функцій?

10. Як викликається функція, що повертає значення void?

11. Як викликається функція, що повертає значення будь-якого типу, який відрізняється від типу void?

12. Значення якого типу повертає функція, якщо тип не вказано?

13. Скільки значень може повернути функція?

Рекурсивні функції
Лабораторна робота 5

Мета роботи.

¾ вивчити особливості рекурсивних процесів

¾ опанувати технологію рекурсивних обчислень

¾ навчитися розробляти алгоритми та програми із застосуванням рекурсивних функцій

5.1 Теоретичні відомості

Означення називається рекурсивним, якщо воно задає елементи множини за допомогою інших елементів цієї самої множини. Об' єкти, що задані рекурсивним означенням, також називаються рекурсивними. Під терміном "рекурсивно задана функція" розуміється така функція, значення якої для данноrо apгумента обчислюється за допомогою значень для попередніх apгументов. При кожній конкретній реалізації процес обчислення такої функції задається рекурентною послідовністю. У практиці обчислень це пов'язано з тим, що, маючи справу з реальною функцією, ми не обчислюємо її в реальному завданні на усій числовій осі, а обчислюємо для деякої кінцевої послідовності значень apгументов.

Рекурсія — це такий спосіб організації обчислювального процесу, за якого функція звертається сама до себе. Такі звернення називаються рекурсивними викликами, а функція, що містить рекурсивні виклики, — рекурсивною.

Перед тим, як записати рекурсивну функцію будь-якою мовою програмування, необхідно записати рекурентне співвідношення, що визначає метод обчислення функцій. Рекурентне співвідношення повинне містити як мінімум дві умови:

¾ умову продовження рекурсії (крок рекурсії);

¾ умову закінчення рекурсії.

Розглянемо функцію , де аргумент є цілим додатним числом, таким, що або . Потрібно обчислити значення членів послідовності Рекурсивне завдання послідовності як послідовності значень функції включає такі два етапи.

1. Функція задається безпосередньо у вигляді числових значень для деякої конечної множини початкових значень аргументу .

2. Задається метод або формула, які дозволяють, знаючи усі значення функції при , обчислити її значення при 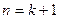, тобто знайти .

В результаті отримуємо peкуррентні співвідношення, що описують рекурсивно задану функцію , рівносильну послідовності .

Отриманий запис цих двох етапів

називається рекурентним співвідношенням.

Рекурсію реалізовують за допомогою виклику функції самої себе. При цьому в тілі функції спочатку слід перевіряти умову продовження рекурсії. Якщо вона істинна, то виходити з функції. Інакше здійснювати рекурсивний крок.

В рекурсивних підпрограмах можна виділити два процеси: рекурсивне занурення підпрограми у себе, що відбувається доти, доки параметр не сягне граничного значення, та рекурсивне повернення з підпрограми, що відбувається доти, доки параметр не сягне початкового значення. Рекурсія реалізує нескінченний цикл, отже застосовувати її слід тільки у випадках, коли без неї неможливо обійтися.

Розглянемо рекурсивну функцію, що обчислює n -й член послідовності чисел Фібоначчі. Ці числа визначаються рекурентним співвідношенням:

Програмний код, що реалізує рекурсивні обчислення, такий:

int Fib(int n)
{
if (n == 0) return 0;
else if (n == 1) return 1;
else return Fib(n–1)+Fib(n–2);
}

Дата добавления: 2015-08-27