Приклад алгоритму та програми. Одним із найпростіших прикладів рекурсії – це функція обчислення факторіала

Одним із найпростіших прикладів рекурсії – це функція обчислення факторіала. Нагадаємо, що факторіалом n! натурального числа n називається добуток усіх цілих чисел від одиниці до n. Вважають також, що 0!=1. Обчислення факторіала зводиться до багаторазового застосування рекурентної формули n! = (n - 1)!· n. Ця формула є рекурсивною, оскільки означує «факторіал через факторіал». Рекурсивне обчислення n! низхідним: «обчислити (n – 1)! і отримане значення помножити на n». При обчисленні (n – 1)! застосоване те саме правило: «обчислити (n – 2)! і отримане значення помножити на n – 1». Рекурсія являє нескінченний цикл, для її переривання необхідно визначити умову завершення рекурсії. Такою умовою буде рівність n нулеві.

Повне рекурсивне означення факторіала:

//ex4_9.cpp. Обчислення факторіала числа
#include<iostream>
using namespace std;
int x; //число, факторіал якого необхідно обчислити
int Factorial(int n) //оголошення функції
{
if (n==0) return 1;
else return Factorial(n-1)*n; //рекурсивний виклик функції
}
int main() //головна функція
{
cout<<"calculate factorial"<<endl;
cout<<"Enter x "<<endl;
cin>>x;
cout<<"x!="<<Factorial(x)<<endl;
system("pause");
}

5.3. Варіанти завдань

1. Знайти суму цифр натурального числа n та значення глибини рекурсії, використовуючи рекурентне означення функції f(n):

Підказка. Умова продовження рекурсії: сума цифр числа дорівнює останній цифрі плюс сума цифр числа без останньої цифри (числа, що ділиться без остачі на 10). Умова закінчення рекурсії: якщо число дорівнює 0, то сума його цифр дорівнює 0.

2. Знайти кількість одиниць в двійковому представленні числа n та значення глибини рекурсії, використовуючи рекурентне означення функції f(n) (& - операція побітового логічного множення):

3. Знайти значення біноміального коефіцієнта при заданих n, k за формулою:

= ,

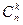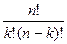використовуючи рекурентне співвідношення:

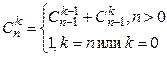
Визначити глибину рекурсії.

4. Знайти значення функції Аккермана A(m, n), використовуючи рекурентне співвідношення:

Визначити глибину рекурсії.

5. Визначити кількість розбиття додатного цілого числа та глибину рекурсії в рекурсивному алгоритмі. Розбиття цілого числа - це його зображення у вигляді суми цілих додатних чисел. Обчислити функцію 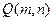, яка визначається як кількість розбиття цілого із доданками, що не перевищують значення . Функція 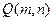визначається за рекурентним співвідношенням:

6. По колу стоять людей, яким присвоєні номери від 1 до . Починаючи відлік з першого і рухаючись по колу, кожна друга людина виходитиме з кола доти, поки не залишиться одна. Нехай номер того, хто залишився, 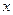. Потім по колу стоятиме 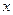людей і процедура виходу з колу людей повторюватиметься доти, поки не залишиться одна людина з номером . Ці процедури повторюватимуться доти, поки номер тої людини, що залишиться, не стане рівним первинній кількості людей в потоковому раунді. Визначити кількість повторень процедури виходу людей з кола після першої ітерації та номер людини, яка залишилася.

Підказка. Використати рекурсію, визначивши рекурентне співвідношення:

7. Визначити рекурсивні функції зображення натурального числа у двійковій, вісімковій системах числення та у системі числення з основою N > 1 та глибину рекурсії. Числа у десятковій системі числення вводити з клавіатури.

8. Визначити рекурсивну функцію обчислення найбільшого спільного дільника НСД{п,т) натуральних чисел, яка ґрунтується на співвідношенні НСД(п,т) = НСД(т,r), де r -залишок від ділення п на т.

9. Визначена рекурсивна функцію через рекурентне співвідношення:

Визначити глибину рекурсії та обчислити функції за заданими значеннями :

10. Визначити рекурсивну функцію обчислення степеня дійсного числа з цілим показником , згідно з рекурентним співвідношенням:

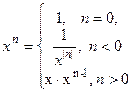
11. Коефіцієнти розкладання бінома (a+b) ⁱ, тобто біноміальні коефіцієнти, утворюють і -й рядок трикутника Паскаля. Кожне число в трикутнику, крім перших трьох, є сумою чисел, розташованих над ним у попередньому рядку. Число в i -му рядку (i = 0, 1, 2, …) на j- му місці (j = 0, 1, …, i), задається формулою . «Верхівка» трикутника має наступний вигляд.

Надрукувати перші рядків трикутника Паскаля із заданою кількістю рядків, використавши рекурсивне визначення його елементів.

12. Написати рекурсивну функцію, яка методом ділення відрізання навпіл (методом дихотомії) знаходить з точністю 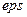корінь рівняння на відрізку (). Згідно з методом дихотомії, якщо i мають різні знаки, то між точками 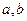існує корінь 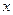. Нехай – середня точка в інтервалі . Якщо , то корінь . Якщо , то або і мають різні знаки, або і мають різні знаки. Якщо , то корінь лежить в інтервалі Інакше він лежить в інтервалі Процес продовжується доти, поки інтервал не стане менший 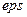. Визначити глибину рекурсії під час обчислення кореня рівняння.

13. Реалізувати генератор послідовності псевдовипадкових чисел { Vi } на основі рекурентного співвідношення V_i = (aV_{i –1} + bV_{i– 2} + c) mod m, де a, b, c, m — довільні натуральні параметри. Перші два значення, V ₁ і V ₂, задаються випадково. Підібрати значення параметрів, за яких послідовність є схожою на випадкову.

14. Довести, що для перших чисел послідовності Фібоначчі
справедлива формула: ,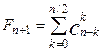

де - біноміальні коефіцієнти, що розраховуються за рекурентним співвідношенням:

Числа Фібоначчі визначаються рекурентним співвідношенням:

15. Для числа, що введено з клавіатури, визначити рекурсивні функції для обчислення суми та кількості його цифр, максимальної та мінімальної цифри. Визначити рекурентні співвідношення та глибину рекурсії.

16. Задати з клавіатури перший член і різницю арифметичної прогресії. Визначити
рекурсивні функції для знаходження -го члена арифметичної прогресії та суми її членів. Визначити рекурентні співвідношення та глибину рекурсії.

17. Задати з клавіатури перший член і знаменник геометричної прогресії. Визначити рекурсивні функції для знаходження -го члена геометричної прогресії та суми її членів. Визначити рекурентні співвідношення та глибину рекурсії.

18. Визначити добуток двох комплексних чисел . Вхідні значення – числа 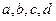. Результат – числа . Використати рекурсивний алгоритм Карацуби.

Підказка. З алгоритмом Карацуби початкові операнди множення подаються як вирази , де для 32-бітних процесорів, визначається як половина розміру (в 32-бітових словах) мінімального по довжині множника. Таким чином, початкові множники розбиваються на молодшу і старшу частині. Після розбиття операндів виконується розрахунок проміжних значень:

Результуючий добуток розраховується за формулою:

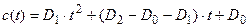
Множення на здійснюється за допомогою зсуву, а підсумовування 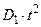та за допомогою конкатенації. Метод Карацуби дозволяє звести операцію множення двох великих чисел до трьох множень чисел половинного розміру (в порівнянні з початковими операндами), п'яти операцій підсумовування і одного зсуву.

19. Потрібно сплатити поштове відправлення, вартість котрого складає копійок, а в наявності тільки поштові марки номіналом копійок. Скількома різними способами можна сплатити поштове відправлення? Розробити рекурсивну функцію для обчислення кількості зображень числа у вигляді суми певних фіксованих чисел з використанням рекурентних співвідношень.

Підказка. Використати рекурентне співвідношення для чисел Фібоначчі.

20. Довести, що рекурсивна послідовність

має межу при і знайти значення цієї межі. Визначити глибину рекурсії під час розрахунку.

21. Задані натуральні числа а, c, m. Визначити рекурсивну функцію та глибину рекурсії для обчислення за формулою:

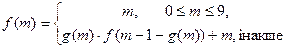, де

- залишок від ділення на 10.

22. Двійкові числа довжини складаються з нулів і одиниць. Нехай – функція, значенням якої є кількість двійкових чисел довжини , що не містять двох або більше одиниць поспіль. Визначити рекурентне співвідношення, яке задає функцію , надрукувати такі числа, підрахувати їх кількість.

23. По заданим b, p, m обчислити значення виразу . Обчислення 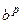виконати, використовуючи алгоритм, що базується на двійковому розкладанні показника степені p:

24. Функція f визначена так:

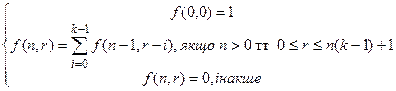
Обчислити значення , якщо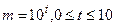

5.4 Контрольні запитання

1. Що таке рекурсивне визначення і рекурсивний об’єкт?

2. Визначити поняття рекурсії. Що таке рекурсивна підпрограма?

3. Як визначається глибина рекурсії?

4. Як обмежити послідовність вкладених викликів рекурсивної підпрограми?

5. Коли рекурсія неефективна і коли її необхідно уникати?

6. Чим викликається переповнення стеку під час рекурсії?

Покажчики
Лабораторна робота 6

Мета роботи.

¾ ознайомитися з особливостями посилальних типів даних;

¾ опанувати технологію застосування посилальних типів даних;

¾ навчитися розробляти алгоритми та програми із застосуванням посилальних типів даних.

6.1 Теоретичні відомості

6.1.1. Основні поняття

До посилальних типів відносяться покажчики та посилання. Покажчики дозволяють працювати з адресами комірок оперативної пам’яті, тим самим вони реалізують непрямий доступ до їх вмісту. Посилання є альтернативними іменами змінних. Застосування покажчиків і посилань як параметрів функцій дозволяє функції змінювати значення своїх аргументів, отже, повертати в програму більше ніж одне значення.

Змінні, що зберігають адреси інших змінних, називаються змінними-покажчиками чи просто покажчиками. Для визначення адреси змінної означена операція & отримання адреси. Якщо оголошена та ініціалізована змінна, наприклад, int value=10, її адресу можна визначити виразом &value. Якщо значення, що зберігаються, займатимуть послідовність байтів, покажчик адресує перший байт цієї послідовності.

6.1.2. Оголошення та ініціалізація

Константні значення, арифметичні вирази та регістрові змінні не зберігають значення в оперативній пам’яті, тому застосувати до них операцію & неприпустимо.

Змінну-покажчик оголошують:

<тип>* <ідентифікатор_­покажчика>;

Тут <тип> — простий чи структурований тип адресованої змінної; <ідентифікатор_­покажчика> — рядок символів, що є ім’ям змінної-покажчика; символ * означає «вказати на».

Покажчик перед використанням iнiцiалiзується адресою змінної або значенням іншого покажчика. Покажчику можна присвоїти значення 0 (NULL). Такий покажчик не адресує жодну змінну.

Посиланняє псевдонімом змінної, тобто її альтернативним іменем і для нього не резервується місце в оперативній пам’яті. Синтаксис оголошення посилання застосовує символ &, який записують після типу змінної:

<тип>& <ідентифікатор_посилання >;

Посилання слід iнiцiалiзувати ім’ям змінної. Типи посилання та змінної, значенням якої ініціалізуються посилання, мають збігатися.

6.1.3. Операції над покажчиками

Для покажчиків означені операції адресування, присвоєння, арифметичні та відношення.

Унарна операція & повертає адресу свого аргументу.

Значення змінної за певною адресою отримують, застосувавши операцію розименування. Операція позначається символом *, який записують перед іменем покажчика. Операція * повертає об’єкт, на який вказує покажчик.

Операція присвоєння використовується для надання значення покажчику

Арифметичні операції: унарні операції інкремента та декремента, бінарні операції додавання та віднімання цілого числа, віднімання одного покажчика з іншого.

Покажчики одного типу можна порівнювати один з одним. При цьому порівнюються адреси, що зберігаються в покажчиках.

Покажчик на функцію містить адресу її в оперативній пам’яті. Ім’я функції — це початкова адреса її коду. До функцій можна застосувати тільки дві операції: виклик і отримання її адреси, тобто визначити її покажчик.

Синтаксис оголошення покажчика на функцію:

<тип> (*<ідентифікатор покажчика>)(<оголошення параметрів>);

Щоб викликати функцію через покажчик, його слід розименувати.

Існують три способи передачі аргументів у функцію — як значення, як посилання та як покажчики. Щоб повертати з функцій більше одного значення, слід передати функції аргументи-посилання або аргументи-покажчики. Під час оголошення функції параметри-посилання вказують у її заголовку, використовуючи операцію посилання &. Параметри-покажчики оголошують в заголовку функції, використовуючи операцію непрямої адресації *.

В операціях виклику функції з аргументом-покажчиком застосовується операція & адресації змінної, значення котрої змінюватимуться. В операції виклику функції з параметром-посилання аргументом є ім’я змінної.

6.1.4. Методи розв’язанні нелінійних рівнянь

Метод перебору. При розв’язанні нелінійного рівняння методом перебору задаються початкове значення аргументу x=a і крок h, який при цьому визначає і точність знаходження коріння нелінійного рівняння. Поки виконується умова F(x)*F(x+h)>0 аргумент x збільшуємо на крок h (x=x+h). Якщо добуток F(x)*F(x+h) стає від’ємним, то на інтервалі [x, x+h] існує розв’язок рівняння.

Метод половинного ділення. При розв’язанні нелінійного рівняння методом половинного ділення задаються інтервал [a, b], на якому існує тільки одне рішення, і бажана точність ε. Потім визначається середина інтервалу с=(а+b)/2 і перевіряється умова F(a)∙F(c)<0. Якщо вказана умова виконується, то праву межу інтервалу b переносимо в середню точку с (b=c). Якщо умова не виконується, то в середню точку переносимо ліву межу(a=c). Ділення відрізку навпіл триває доки |b - a|>ε..

Метод хорд. При розв’язанні нелінійного рівняння методом хорд задаються інтервал [a, b], на якому існує тільки одне рішення, і точність ε. Потім через дві точки з координатами (a, F(a)) і (b, F(b)) проводимо відрізок прямої лінії (хорду) і визначаємо точку перетину цієї лінії з віссю абсцис (точка c). Якщо при цьому F(a)∙F(c)<0, то праву межу інтервалу переносимо в точку с (b=c). Якщо вказана умова не виконується, то в точку c переноситься ліва межа інтервалу (а=с). Пошук рішення припиняється, коли досягається задана точність |F(c)|< ε. Для визначення точки перетину хорди з віссю абсцис використовується формула .

Метод дотичних. При розв’язанні нелінійного рівняння методом дотичних задаються початкове значення аргументу x0 і точність ε. Потім в точці(x0, F(x0)) проводимо дотичну до графіка F(x) і визначаємо точку перетину дотичної з віссю абсцис x1. У точці (x1, F(x1)) знову будуємо дотичну, знаходимо наступне наближення шуканого рішення x2 і так далі. Вказану процедуру повторюємо доки |F(xi)|> ε. Для визначення точки перетину (i+1) дотичної з віссю абсцис використовується формула Умова збіжності методу дотичних .

Дата добавления: 2015-08-27