Приклад алгоритму та програми. Обчислити суму ряду, елемент котрого розраховується за формулою

Обчислити суму ряду, елемент котрого розраховується за формулою

//ex3.1

#include<iostream>

#include<iomanip>

#include<math.h>

using namespace std;

float x; //параметр зовнішньої суми

float k=0; //параметр внутрішньої суми

float sum=0;//сума ряду

float error; //точність розрахунків

float member; //елемент ряду

//=======обчислення факторіала числа=========

float factorial(int number)

{ //параметр number– число, факторіал котрого розраховується

float fact=1;

if (number==0) fact=1;

else

{

for(int i=1;i<=number;i++)

fact*=i;

}

return (float)fact;

}

///===========виведення поточних розрахунків===========

void OutputSum()

{

cout<<setw(5)<<x<<setw(10)<<k<<setw(20)<<member<<setw(15)<<sum<< endl;

}

//===========обчислення елемента ряду та суми==============

void MemberAndSum()

{

double Numerator; //чисельник елемента ряду

double Denominator; //знаменник елемента ряду

for (x=1;x<=5;x++)

{

k=0;

do

{

Numerator=pow(x,(2*k-1));

if(k>16) //floating point error - overflow

{

cout<<"overflow - break cycle with k"<<endl;

break;

}

else

{

Denominator=(2*k-1)*factorial(2*k+1);

member=(float)Numerator/Denominator;

member*=(-1);

sum+=member;

OutputSum();

k++;

}

}while(fabs(member)<error); //поки не досягнуто

// заданої точності

}

}

/////// головна функція////////////

int main()

{

cout<<"To calculate the sum of row "<<endl;

cout<<" 5 endlessness "<<endl;

cout<<" sum (sum (((-1)^(k+1))*(x^(2k-1))/((2k-1)(2k+1)!)))" <<endl;

cout<<" x=1 k=0"<<endl;

cout<<"input error: ";

cin>>error;

cout<<"result of iterations"<<endl;

cout<<"=================================================="<<endl;

cout<<" x k member sum "<<endl;

cout<<"=================================================="<<endl;

MemberAndSum();

cout<<"=================================================="<<endl;

cout<<"sum="<<sum<<endl;

system("pause");

}

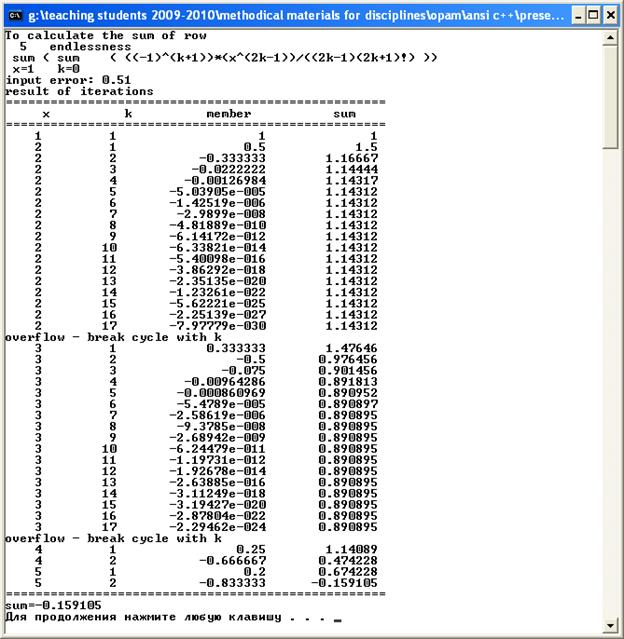
Рис. 3.1. Результати роботи програми ex3.1

3.3. Варіанти завдань

1.	12.
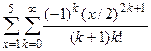
2.	13.
3.	14.
4.	15.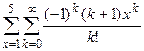
5.	16.
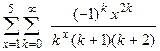
6.	17.
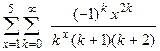
7.	18.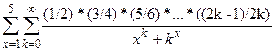
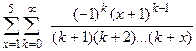
8.	19.
9.	20.
10.	21.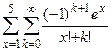
11.	22.

3.4 Контрольні запитання

1. У чому полягає відмінність між циклами з передумовою та циклами з постумовою?

2. Якому типу даних може належати лічильник у циклі for?

3. Яке значення має лічильник після завершення циклу for?

4. Що може спричинити «зациклення» програми?

5. За яких умов цикли while та for не виконаються жодного разу?

6. Коли цикл виконується лише один раз?

7. У чому полягає відмінність між такими операторами циклів, як for, while, do … while?

8. Поясність алгоритм роботи вкладених циклів.

9. Якщо оператор break розміщується у внутрішньому циклі, то який цикл він перериває?

10. За яких умов слід обирати цикли for та while?

Цикли з розгалуженням
Лабораторна робота 4

Мета роботи.

– вивчити особливості циклічних обчислювальних процесів з розгалуженнями

– опанувати технологію рекурентних обчислень

– навчитися розробляти алгоритми та програми розвинення функцій у ряди

4.1 Теоретичні відомості

4.1.1. Рекурентні співвідношення

Формула, що виражає член послідовності через один або декілька попередніх, називається рекурентним співвідношенням. Послідовність, члени якої задовольняють деякому рекурентному співвідношенню, називається рекурентною.

У загальному випадку рекурентне співвідношення визначає залежність члена послідовності { S_n } від k попередніх: S_n = F (S_{n – k} ,..., S_{n –1}).

Наближене значення суми ряду можна отримати або обмежуючись сумою перших n його членів, або обчислюючи суму з наперед заданою точністю. Формула загального члена даного ряду є достатньо простою, але використовувати її не раціонально, оскільки для кожного члена ряду треба обчислювати степінь і факторіал. Набагато вищої ефективності можна досягти, обчислюючи член ряду за допомогою рекурентного співвідношення. Найпростішими прикладами рекурентних послідовностей є арифметична та геометрична прогресії, елементи яких пов’язані з попередніми елементами співвідношеннями a_n = a_{n –1} + d та a_n = a_{n –1} · q, де d та q — деякі сталі величини, a_n – значення елемента ряду на кроці n.

Із заданою точністю може бути обчислена сума лише збіжного ряду, а довільний степеневий ряд має певну область збіжності (можливо, порожню), тобто збігається не за всіх, а лише за деяких значень x (ряд, що розглядається нами як приклад, збігається для будь-якого дійсного x). По-друге, простий спосіб перевірки точності часткової суми ряду існує не для всіх рядів. Такий спосіб існує, зокрема, для знакопереміжних рядів, абсолютні величини членів яких, починаючи з деякого номера, утворюють монотонно спадну послідовність. Для таких рядів сума всіх членів, починаючи від (n +1)-го, є меншою за модулем від n -го

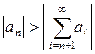
4.1.2. Функції користувача

Функція користувача містить оператори, що логічно не залежать від іншого коду програми, і може викликатися з будь-якого місця програми довільну кількість разів. Формат функції визначає її заголовок та тіло, яке містить оператори відповідно до алгоритму. Визначення функції передбачає наявність заголовка та тіла. Функцію без заданого прототипу визначають перед функціями, які її викликають, а ту, що має прототип, можна визначати в будь-якому місці програми. Функція має повернути тільки одне визначене значення до основної програми. Тип значення, що повертається, визначається у заголовку функції.

Оголошення функції (прототип) задається у вигляді:

тип_значення_що_повертається ім'я_функції (тип_параметра ім'я_параметра1, тип_параметра ім'я_параметра2);

Визначення функції містить її код виконання. Заголовки функції при оголошенні та визначенні збігаються. Не ставиться символ; наприкінці заголовка. Для повернення значення з функції в тілі функції необхідно мати оператор повернення return.

Приклад визначення найбільшого з двох чисел:

float max(float a,float b) //заголовок функції з параметрами
{

float m; //найбільше значення
m =(a>b)?a:b; //умовний вираз
return m; //значення, що визначилося та повертається

}

Функцію можна оголосити у вигляді:

void ім'я_функції(void);

Тип void значення, що повертається, означає, що така функція не повертає ніякого значення. Оператор return не потрібний. Тип void у списку параметрів означає, що функція не має параметрів.

Функція виконує закодовані в ній дії за допомогою оператора виклику. У процесі визначення функції у заголовку описуються формальні параметри, які замінюються на аргументи під час виклику функції. Якщо функція не повертає значення у точку виклику, формат оператора її виклику має такий вигляд:

ім'я_функції(аргументи);

Якщо функція повертає будь-яке значення, то під час її виклику це значення треба присвоїти змінній відповідного типу. Формат оператора виклику такий:

ім'я_змінної = ім'я_функції(аргументи);

Для виконання лабораторної роботи необхідно використовувати ряди, які представляють функції (табл. 4.1).

Таблиця 4.1 Рекурентні формули розвинення функцій у ряди

Функції	Розвинення у ряд Тейлора
sin(x)	x - x^3/3! + x^5/5! - x^7/7! +...
cos(x)	1 - x ^2/2! + x^4/4! - x^6 /6! +...
arctg(x)	x - x^3/3 + x^5/5 - x^7/7 +...
ln (x)	(x-1) - (x-1)^2/2 + (x-1)^3/3 - (x-1)^4/4+...
e^x	1 + x / 1! + x^2/ 2! + x^3 / 3! +...
e^-x	1 - x/1! + x^2/2! - x^3/3! + x^4/4!-...
sh (x)	x + x^3/3! + x^5/5! + x^7/7! +...
x^1/2	y0=1, yn+1 = 1/2*(yn+x/yn), n = 0, 1, 2,…

Дата добавления: 2015-08-27