Расчет по раскрытию трещин

Этот расчет выполняют для сечения, в котором значение растягивающих напряжений в бетоне наибольшее.

Ширину раскрытия продольных трещин определяем по формуле (согласно [1] п.3.105)

а_сч= , где Δσ_р – приращение напряжений после погашения обжатия бетона.

Е_р – модуль упругости напрягаемой арматуры;

Ψ – коэффициент раскрытия трещин

Δσ_р= где σ_bt,z-растягивающее напряжение в бетоне на уровни ц.т. растянутой арматуры;

μ_р- коэффициент армирования

высота растянутой зоны бетона определяется из эпюры нормальных напряжений.

Схема и эпюра нормальных напряжений к расчету

раскрытия поперечных трещин балки.

Растягивающие напряжение в нижней грани балки σ_bt определены при расчете нормальных напряжений на трещиностойкость.

Сжимающее напряжения по верхней грани сечения находим при способе напряжения на упоры по формуле:

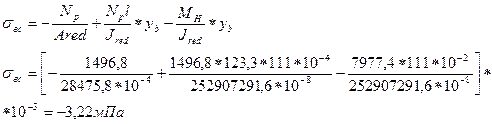
σ_вс≤R_b,sec, где R_b,sec – расчетное сопротивление бетона осевому сжатию, R_b,sec=23мПа

-3,22мПа<23мПа

Высоту растянутой зоны находим из выражения

Вычисляем статистический момент растянутой зоны относительно нейтральной оси:

Определяем положение центра тяжести:

Находим коэффициент армирования

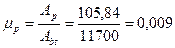
Коэффициент раскрытия трещин для арматурных пучков из гладкой проволоки определяем из выражения:

Ψ=1,5 , где R_r – радиус армирования

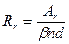, где А_r- площадь взаимодействия арматуры и бетона;

β – коэффициенты сцепления арматуры и бетона

n – количество пучков;

d – диаметр арматурного пучка.

Площадь зоны взаимодействия ограничивается наружным контуром сечения и радиусом взаимодействия (r=5d=5*6=30см)

A_r= 29*150+1*50=4400см²

R_r= =162,9

Ψ= 1,5* 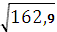=19

a_cr= =0,014 см

Δ_cr по [1] принимается 0,015см

А_cr= 0,014 см< Δ_cr =0,015см

Условие удовлетворяется

Дата добавления: 2015-08-27